Bài 1.12: Một vật dao động điều hoà theo phương trình x = 0,05cos10\(\pi\)t (m). Hãy xác định :
a) Biên độ, chu kì và tần số’của vật.
b) Tốc độ cực đại và gia tốc cực đại của vật.
c) Pha của dao động và li độ của vật tại thời điểm t = 0,075 s.
chi tiết
a) – Biên độ dao động của vật là A = 0,05m
– Chu kỳ của dao động là T = 2\(\pi\):\(\omega\) = 2\(\pi\):10\(\pi\) = 0,2s
– Tần số dao động của vật là f = 1: T= 1: 0,2= 5Hz
b) Vận tốc cực đại của vật là \({v_{\max }} = \omega A = 10\pi .0,05 = 0,5\pi \) m/s
Gia tốc cực đại của vật là \({a_{\max }} = \omega^2 A = (10\pi)^2 .0,05 = 5\pi^2 \) \(m/s^2\)
c) Pha dao động của vật ở li độ t = 0,075s là : 10\(\pi\)t = 10\(\pi\).0,075 = \({3\pi \over 4}\)
Li độ của vật là x = 0,05cos\({3\pi \over 4}\)=- 0,035m
Bài 1.13: Một vật dao động điều hoà với biên độ A = 24 cm và chu kì T = 4 s. Tại thời điểm t = 0, vật có li độ cực đại âm (x = -A).
Advertisements (Quảng cáo)
a) Viết phương trình dao động của vật.
b) Tính li độ, vận tốc và gia tốc của vật tại thời điểm t = 0,5 s.
c) Xác định thời điểm đầu tiên vật qua vị trí có li độ x = -12 cm và tốc độ tại thời điểm đó.
a) Viết phương trình dao động của vật
A = 24cm; T= 4s=> \(\omega\) =\({2\pi \over T} ={{\pi \over 2}}\); Tại thời điểm ban đầu vật ở biên âm nên ta có \(\varphi \) = \(\pi\)
Nên phương trình dao động của vật là : x= 24cos(\({{\pi \over 2}}t\)+\(\pi\)).
Advertisements (Quảng cáo)
b) Tai thời điểm t = 0,5s ta có
Li độ: x = 24.cos(\({{\pi \over 2}}.0,5\)+\(\pi\)) = 24.cos\( 5\pi\over4\)=-16,9 cm \( \approx \) 17 cm
Vận tốc : v = – 24.\(\pi \over 2\)sin (\({{\pi \over 2}}.0,5\)+\(\pi\)) = – 24.\(\pi \over 2\)sin\( 5\pi\over4\)= 6\(\pi \sqrt2\) cm/s =26,64 cm/s \( \approx \) 27 cm/s
Gia tốc : a =-\(({\pi \over 2})^2\).x= -\(({\pi \over 2})^2\).(-16,9) = 41,6 cm/s2\( \approx \) 42 (cm/s2)
c) Thời điểm đầu tiên vật đi qua li độ x = -12 cm là
x = 24cos(\({{\pi \over 2}}t\)+\(\pi\)) = -12
⇒ cos(\({{\pi \over 2}}t\)+\(\pi\)) = -\(1\over2\)
⇒ (\({{\pi \over 2}}t\)+\(\pi\)) = (\({{\pi \over 3}}\)+\(\pi\))
⇒ \({{\pi \over 2}}t\)= \({{\pi \over 3}}\)
⇒ t =\(2\over3\) s \( \approx \) 0,67s
Tốc độ tại thời điểm t =\(2\over3\) s là
v = -\(\omega A\)sin(\({{\pi \over 3}}\)+\(\pi\)) = 32,6 cm/s \( \approx \) 33 cm
Bài 1.14: Xét một cơ chế truyền và biến đổi chuyển động (H.1.1). Hãy giải thích tại sao khi bánh xe quay đều thì pit-tông dao động điều hoà
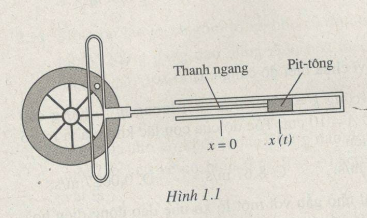
Thanh ngang trùng với trục Ox. Hình chiều của quả cầu trên trục Ox trùng với đầu thanh ngang. Do đó khi quả cầu chuyển động tròn đều thì thanh ngang và pít – tông dao động điều hòa
Bài 1.15: Chọn trục x làm gốc để tính pha (H.1.2). Chứng minh rằng dao động của điểm P trên trục x theo phương trình x = Acos\(\omega\)t và dao động của điểm Q trên trục y theo phương trình y = Asin(\(\omega t +{\pi\over2}\)) là giống hệt nhau.
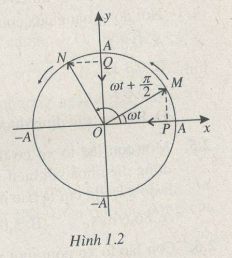
Theo hình H.1.2 vì cos\(\omega\) = sin(\(\omega t +{\pi\over2}\)) nên dao động của điểm P trên trục x giống dao động của điểm Q tên trục y.
