Bài 60 : a) Chứng minh rằng đồ thị của hai hàm số \(y = {a^x};\,y = {\left( {{1 \over a}} \right)^x}\) đối xứng với nhau qua trục tung.
b) Chứng minh rằng đồ thị của hai hàm số \(y = {\log _a}x;\,\,y = {\log _{{1 \over a}}}x\) đối xứng với nhau qua trục hoành.
Giải
a) Gọi \(\left( {{G_1}} \right)\) và \(\left( {{G_2}} \right)\) lần lượt là đồ thị củ hàm số \(y = {a^x};\,y = {\left( {{1 \over a}} \right)^x}\), \(M\left( {{x_o},{y_o}} \right)\) là một điểm bất kì. Khi đó điểm đối xứng với M qua trục tung là \(M’\left( { – {x_o},{y_o}} \right)\).
Ta có: \(M \in \left( {{G_1}} \right) \Leftrightarrow {y_o} = {a^{{x_o}}} \Leftrightarrow {y_o}={\left( {{1 \over a}} \right)^{ – {x_o}}} \)
\(\Leftrightarrow M’ \in \left( {{G_2}} \right)\)
Điều đó chứng tỏ \(\left( {{G_1}} \right)\) và \(\left( {{G_2}} \right)\) đối xứng với nhau qua trục tung.
b) Gọi \(\left( {{G_1}} \right)\) và \(\left( {{G_2}} \right)\) lần lượt là đồ thị củ hàm số \(y = {\log _a}x;\,\,y = {\log _{{1 \over a}}}x\)
Lấy \(M\left( {{x_o},{y_o}} \right)\) tùy ý. Điểm đối xứng với M qua trục hoành là \(M’\left( {{x_o}, – {y_o}} \right)\).
Ta có: \(M \in \left( {{G_1}} \right) \Leftrightarrow {y_o} = {\log _a}{x_o} = – {\log _{{1 \over a}}}{x_o} \)
\(\Leftrightarrow – {y_o} = {\log _{{1 \over a}}}{x_o} \Leftrightarrow M’ \in \left( {{G_2}} \right)\)
Vậy \(\left( {{G_1}} \right)\) và \(\left( {{G_2}} \right)\) đối xứng với nhau qua trục hoành.
Bài 61: SGK giải tích 12 nâng cao: a) Vẽ đồ thị hàm số \(y = {\log _{0,5}}x > 0;\)
b) \( – 3 \le {\log _{0,5}}x \le – 1\)
Advertisements (Quảng cáo)
Giải: a) TXĐ: \(D = \left( {0; + \infty } \right)\)
a = 0,5 < 1. Hàm số nghịch biến trên \(\left( {0; + \infty } \right)\).
Bảng giá trị:
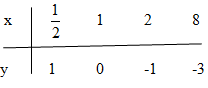
Advertisements (Quảng cáo)
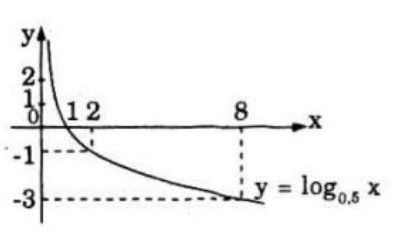
b) \({\log _{0,5}}x > 0 \Leftrightarrow 0 < x < 1\) (ứng với phần đồ thị ở phía trên trục hoành).
c) \( – 3 < {\log _{0,5}}x < – 1 \Leftrightarrow 2 < x \le 8\) (ứng với những điểm trên đồ thị có tung độ thuộc nửa khoảng \(\left[ { – 3;1} \right)\)).
Bài 62: SGK giải tích 12 nâng cao: Vẽ đồ thị của hàm số \(y = {\left( {\sqrt 3 } \right)^x}\). Dựa vào đồ thị, hãy giải thích các bất phương trình sau:
a) \({\left( {\sqrt 3 } \right)^x} \le 1\); b) \({\left( {\sqrt 3 } \right)^x} > 3\)
Giải
TXĐ: \(D =\mathbb R\)
Hàm số đồng biến trên R.
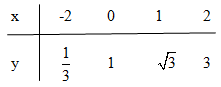
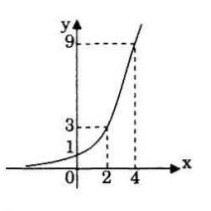
a) \({\left( {\sqrt 3 } \right)^x} \le 1 \Leftrightarrow x \le 0\) (ứng với những điểm trên đồ thị có tung độ lớn hơn 1)
b) \({\left( {\sqrt 3 } \right)^x} > 3 \Leftrightarrow x > 2\) (ứng với những điểm trên đồ thị có tung độ lón hơn 3).

