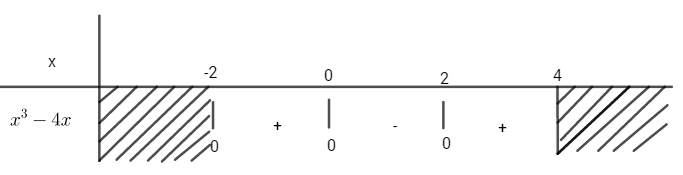Bài 26: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {\mathop{\rm s}\nolimits} {\rm{inx}} + 1\), trục hoành và hai đường thẳng \(x=0\) và \(x = {{7\pi } \over 6}\)
Giải: Vì \({\mathop{\rm s}\nolimits} {\rm{inx}} + 1 \ge 0\) với mọi \(x\) nên
\(S = \int\limits_0^{{{7\pi } \over 6}} {\left( {{\mathop{\rm s}\nolimits} {\rm{inx}} + 1} \right)} dx = \left. {\left( { – \cos x + x} \right)} \right|_0^{{{7\pi } \over 6}}\)
\(= {{7\pi } \over 6} + {{\sqrt 3 } \over 2} + 1\)
Bài 27: Tính diện tích hình phẳng giới hạn bởi:
a) Đồ thị hàm số \(y = {\cos ^2}x,\) trục hoành, trục tung và đường thẳng \(x = \pi ;\)
b) Đồ thị hai hàm số \(y = \sqrt x \) và \(y = \root 3 \of x ;\)
c) Đồ thị hàm số \(y = 2{x^2}\) và \(y = {x^4} – 2{x^2}\) trong miền \(x \ge 0.\)
Giải: a) \(S = \int\limits_0^\pi {{{\cos }^2}xdx = {1 \over 2}} \int\limits_0^\pi {\left( {1 + \cos 2x} \right)} dx\)
\(= \left. {{1 \over 2}\left( {x + {1 \over 2}\sin 2x} \right)} \right|_0^\pi = {\pi \over 2}\)
b) Phương trình hoành độ giao điểm của hai đồ thị là \(\sqrt x = \root 3 \of x \Leftrightarrow x = 0;x = 1\)
Trên đoạn \(\left[ {0;1} \right]\) thì \(\root 3 \of x \ge \sqrt x \) nên:
\(S = \int\limits_0^1 {\left( {\root 3 \of x – \sqrt x } \right)} dx = \int\limits_0^1 {\left( {{x^{{1 \over 3}}} – {x^{{1 \over 2}}}} \right)} dx\)
\(= \left. {\left( {{3 \over 4}{x^{{4 \over 3}}} – {2 \over 3}{x^{{3 \over 2}}}} \right)} \right|_0^1 = {3 \over 4} – {2 \over 3} = {1 \over {12}}\)
c) Trong miền \(x \ge 0\) hoành độ giao điểm của hai đồ thị là nghiệm phương trình:
\(\left\{ \matrix{
x \ge 0 \hfill \cr
{x^4} – 2{x^2} = 2{x^2} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x \ge 0 \hfill \cr
{x^2}\left( {{x^2} – 4} \right) = 0 \hfill \cr} \right.\)
Advertisements (Quảng cáo)
\(\Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 2 \hfill \cr} \right.\)
Ta có: \(S = \int\limits_0^2 {\left| {{x^4} – 2{x^2} – 2{x^2}} \right|} dx = \int\limits_0^2 {\left| {{x^2}\left( {{x^2} – 4} \right)} \right|} dx \)
\(= \int\limits_0^2 {\left( {4{x^2} – {x^4}} \right)} dx\)
\( = \left. {\left( {4{{{x^3}} \over 3} – {{{x^5}} \over 5}} \right)} \right|_0^2 = {{64} \over {15}}\)
Bài 28: Tính diện tích hình phẳng giới hạn bởi:
a) Đồ thị các hàm số \(y = {x^2} – 4\), \(y = – {x^2} – 2x\) và đường thẳng \(x = – 3,x = – 2;\)
b) Đồ thị hai hàm số \(y = {x^2}\) và \(y = – {x^2} – 2x\)
c) Đồ thị hàm số \(y = {x^3} – 4x\), trục hoành, đường thẳng x=-2 và đường thẳng x=4
Advertisements (Quảng cáo)
Giải: a) Ta có
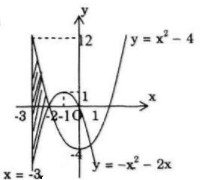
\(S = \int\limits_{ – 3}^{ – 2} {\left| {{x^2} – 4 – \left( { – {x^2} – 2x} \right)} \right|} dx \)
\(= \int\limits_{ – 3}^{ – 2} {\left( {2{x^2} + 2x – 4} \right)} dx\)
\( = 2\int\limits_{ – 3}^{ – 2} {\left( {{x^2} + x – 2} \right)} dx\) vì \(({x^2} + x – 2 \ge 0 \Leftrightarrow x \le – 2\) hoặc \(x \ge 1)\)
\( = 2\left. {\left( {{{{x^3}} \over 3} + {{{x^2}} \over 2} – 2x} \right)} \right|_{ – 3}^{ – 2} = {{11} \over 3}\)
b)Phương trình hoành độ giao điểm của hai đồ thị là:
\({x^2} – 4 = – {x^2} – 2x \Leftrightarrow {x^2} + x – 2 = 0 \Leftrightarrow \left[ \matrix{
x = – 2 \hfill \cr
x = 1 \hfill \cr} \right.\)
Do đó \(S = \int\limits_{ – 2}^1 {\left| {{x^2} – 4 – \left( { – {x^2} – 2x} \right)} \right|} dx \)
\(= \int\limits_{ – 2}^1 {\left| {2{x^2} + 2x – 4} \right|} dx\)
\( = – \int\limits_{ – 2}^1 {\left( {2{x^2} + 2x – 4} \right)} dx\) ( vì \( – 2 \le x \le 1 \Leftrightarrow 2{x^2} + 2x – 4 \le 0\))
\( = \int\limits_{ – 2}^1 {\left( { – 2{x^2} – 2x + 4} \right)} dx \)
\(= \left. {\left( { – {{2{x^3}} \over 3} – {x^2} + 4x} \right)} \right|_{ – 2}^1 = 9\)
c) \(S = \int\limits_{ – 2}^4 {\left| {{x^3} – 4x} \right|} dx \)
\(= \int\limits_{ – 2}^0 {\left( {{x^3} – 4x} \right)} dx – \int\limits_0^2 {\left( {{x^3} – 4x} \right)} dx \)
\(+ \int\limits_2^4 {\left( {{x^3} – 4x} \right)} dx = 44\)