Bài 5: Trong mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức \(z\) thỏa mãn điều kiện:
a) phần thực của \(z\) bằng \(1\)
b) phần ảo của \(z\) bằng \(-2\)
c) Phần thực của \(z\) thuộc đoạn \([-1, 2]\), phần ảo của \(z\) thuộc đoạn \([0, 1]\)
d) \(|z| ≤ 2\)
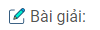
Tập hợp các điểm biểu diễn các số phức z là các hình sau:
a) Ta có \(x = 1, y\) tùy ý nên tập hợp các điểm biểu diễn \(z\) là đường thẳng \(x = 1\)
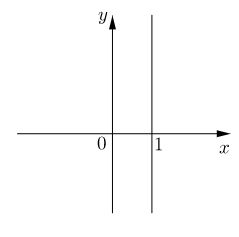
b) Ta có \(y = -2, x\) tùy ý nên tập hợp các điểm biểu diễn \(z\) là đường thẳng \(y = -2\)
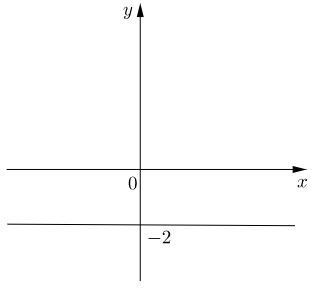
c) Ta có \(x ∈ [-1, 2]\) và \(y ∈ [0, 1]\) nên tập hợp các điểm biểu diễn \(z\) là hình chữ nhật sọc
d) Ta có:
Advertisements (Quảng cáo)
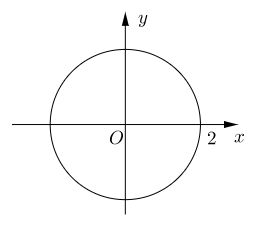
\(\left| z \right| \le 2 \Leftrightarrow \sqrt {{x^2} + {y^2}} \le 2 \Leftrightarrow {x^2} + {y^2} \le 4\)
Vậy tập hợp các điểm biểu diễn \(z\) là hình tròn tâm \(O\) (gốc tọa độ) bán kính bằng \(2\) (kể cả các điểm trên đường tròn)
Bài 6: Tìm các số thực \(x, y\) sao cho:
a) \(3x + yi = 2y + 1 + (2-x)i\)
b) \(2x + y – 1 = (x – 2y – 5)i\)
a)
Advertisements (Quảng cáo)
\(\eqalign{
& 3x + yi = (2y + 1)+(2 – x)i \cr
& \Leftrightarrow \left\{ \matrix{
3x = 2y + 1 \hfill \cr
y = 2 – x \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = 1 \hfill \cr
y = 1 \hfill \cr} \right. \cr} \)
b)
\(\eqalign{
& 2x + y – 1 = (x + 2y – 5)i \cr
& \Leftrightarrow \left\{ \matrix{
2x + y – 1 = 0 \hfill \cr
x + 2y – 5 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = – 1 \hfill \cr
y = 3 \hfill \cr} \right. \cr} \)
Bài 7: Chứng tỏ rằng với mọi số phức \(z\), ta luôn có phần thực và phần ảo của \(z\) không vượt quá môdun của nó.
Giả sử \(z = a + b\)i
Khi đó: \(\left| z \right| = \sqrt {{a^2} + {b^2}}\)
Từ đó suy ra:
\(|z| \ge \sqrt {{a^2}} = |a| \ge a,|z| \ge \sqrt {{b^2}} = |b| \ge b\)
Bài 8: Thực hiện các phép tính sau:
a) \((3 + 2i)[(2 – i) + (3 – 2i)]\)
b) \((4 – 3i) + {{1 + i} \over {2 + i}}\)
c) \((1 + i)^2 – (1 – i)^2\)
d) \({{3 + i} \over {2 + i}} – {{4 – 3i} \over {2 – i}}\)
a) \((3 + 2i)[(2 – i) + (3 – 2i)]= (3 + 2i)(5 – 3i) = 21 + i\)
b)
\(\eqalign{
& (4 – 3i) + {{1 + i} \over {2 + i}} = (4 – 3i) + {{(1 + i)(2 – i)} \over 5} = (4 – 3i)({3 \over 5} + {1 \over 5}i) \cr
& = (4 + {3 \over 5}) – (3 – {1 \over 5})i = {{23} \over 5} – {{14} \over 5}i \cr} \)
c) \((1 + i)^2 – (1 – i)^2 = 2i – (-2i) = 4i\)
d)
\(\eqalign{
& {{3 + i} \over {2 + i}} – {{4 – 3i} \over {2 – i}} = {{(3 + i)(2 – i)} \over 5} – {{(4 – 3i)(2 + i)} \over 5} \cr
& = {{7 – i} \over 5} – {{11 – 2i} \over 5} = {{ – 4} \over 5} + {1 \over 5}i \cr} \)

