Bài 22.8: Chùm hạt a có vận tốc đầu v0 = 0, được giạ tốc qua hiệu điện thế 1,0.106 V, bay vào một từ trường đều có cảm ứng từ 1,5.10-3T. Vận tốc của mỗi hạt a đều hướng vuông góc với các đường sức từ. Hạt a là hạt nhân heli (\({}_2^4He\)) có điện tích q= 3,2.10-19 C và khối lượng m = 6,642.10-27 kg. Xác định lực Lo-ren-xơ do từ trường tác dụng lên mỗi hạt α.
Sau khi được gia tốc qua hiệu điện thế U= 1,0.106 V, vận tốc của mỗi hạt α tính theo công thức :
\({{m{v^2}} \over 2} = qU \Rightarrow v = \sqrt {{{2qU} \over m}} \)
Thay số, ta có
\(v = \sqrt {{{{{2.3,2.10}^{ – 19}}{{.1,0.10}^6}} \over {{{6,642.10}^{ – 27}}}}} = {9,8.10^6}m/s\)
Áp dụng công thức tính lực Lo – ren – xơ f = qvB ta tìm được:
f = qvB = 3,2.10-19.9,8.106.1,5.10-3 = 4,7.10-15N
Advertisements (Quảng cáo)
Bài 22.9: Prôtôn và êlectron có cùng vận tốc và bay vào trong một từ trường đều theo phương vuông góc với các đường sức từ. Prôtôn có điện tích 1,6.10-19 C và khối lượng 1,672.10-27 kg ; êlectron có điện tích -1,6.10-19 C và khối lượn; 9,1.10-31 kg. Hỏi bán kính quỹ đạo tròn của prôtôn lớn hơn bao nhiêu lần bán kính quỹ đạo tròn của êlectron khi các hạt điện tích này chuyển động trong từ trường đều dưới tác dụng của lục Lo-ren-xơ ?
Áp dụng công thức \(R = {{mv} \over {|q|B}}\) ta suy ra bán kính quỹ đạo tròn của proton và electronchuyeenr động với cùng vận tốc \(\overrightarrow v \) trong từ trường đều:
\({R_1} = {{{m_1}v} \over {eB}};{R_2} = {{{m_2}v} \over {eB}}\)
Advertisements (Quảng cáo)
So sánh các bán kính quỹ đạo tròn này ta tìm được:
\({{{R_1}} \over {{R_2}}} = {{{m_1}} \over {{m_2}}} = {{{{1,672.10}^{ – 27}}} \over {{{9,2.10}^{ – 31}}}} = 1840\)
Bài 22.10*: Hạt điện tích q = 1,0.10-6 C chuyển động với vận tốc 500 m/s dọc theo một đường thẳng song song với một dây dẫn thẳng dài vô hạn, cách dây dãn này một khoảng 100 mm. Trong dây dẫn có dòng điện cường độ 2,0 A chạy theo chiều chuyển động của hạt điện tích. Xác định hướng và độ lớn của lực từ tác dụng lên hạt điện tích.
Giả sử ở thời điểm t, hạt điện tích q nằm tại vị trí M cách dòng điện I chạy trong dây dẫn thẳng một khoảng r = 100 mm (Hình 22.1 G). Khi đó dòng điện I gây ra tại điểm M một từ trường có cảm ứng từ tính theo công thức : B = 2.10-7I/r.
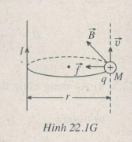
Vec tơ \(\overrightarrow B \) vuông góc với mặt phẳng chứa dòng điện I và điểm M, tức là \(\overrightarrow B \bot \overrightarrow v \). Theo quy tắc bàn tay trái, lực Lo – ren – xơ do từ trường của dòng điện I tác dụng lên hạt điện tích q có phương vuông góc với cả và , có chiều hướng về dòng điện I, có độ lớn bằng:
f = qvB = qv.2.10-7I/r
Thay số, ta tìm được:
\(f = {2.10^{ – 7}}.{{2,0} \over {{{100.10}^{ – 3}}}}{.1,0.10^{ – 6}}.500 = {2,0.10^{ – 9}}N\)

