30.5. Nếu L1 và L2 đều là thấu kính phân kì thì điểm trùng nhau của F1’ và F2 có vị trí :
A. (1) B. (2) c. (3). D.(4).
Đáp án D
30.6. Có hệ hai thấu kính ghép đồng trục L1 và L2. Một tia sáng song song với trục chính truyền qua thấu kính như Hình 30.2. Có thể kết luận những gì về hệ này ?
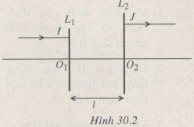
A. L1 và L2 đều là thấu kính hội tụ.
B. L1 và L2 đều là thấu kính phân kì.
C. L1 là thấu kính hội tụ, L2 là thấu kính phân kì.
D. L1 là thấu kính phân kì, L2là thấu kính hội tụ.
Đáp án D
30.7. Tiếp Câu hỏi 30.6, tìm kết luận sai dưới đây về hệ ghép này.
A. F1’ =F2. B.O1O2 = f2 – f1
C. IJ kéo dài cắt trục chính tại F2 D. O1O2 = f1 + f2
Đáp án B
Bài 30.8: Cho một hệ gồm hai thấu kính L1 và L2 đồng trục. Các tiêu cự lần lượt là : f1 = 20 cm; f2 = – 10 cm. Khoảng cách giữa hai quang tâm O1O2 = a = 30 cm. Vật phẳng nhỏ AB đặt trên trục chính, vuông góc với trục chính và ở trước L1, cách L1 là 20 cm.
Advertisements (Quảng cáo)
a) Xác định ảnh sau cùng của vật, vẽ ảnh.
b) Tìm vị trí phải đặt vật và vị trí của ảnh sau cùng biết rằng ảnh này là ảo và bằng hai lần vật.
\(\begin{array}{l}
AB{A_1}{B_1}A’B’\\
{d_1} = 20cm = {f_1};{d_1}’ \to \infty \\
{d_2} = a – {d_1}’ \to – \infty ;{d_2}’ = {f_2} = – 10cm
\end{array}\)
Ảnh ảo cách O2 một đoạn 10cm
\(k = {k_1}{k_2} = \left( { – \frac{{{d_1}’}}{{{d_1}}}} \right)\left( { – \frac{{{d_2}’}}{{{d_2}}}} \right) = \frac{{{d_2}’}}{{{d_1}}}\frac{{{d_1}’}}{{{d_2}}} = \left( {\frac{{{d_2}’}}{{{d_1}}}} \right)\frac{{{d_1}’}}{{a – {d_1}’}} = \left( {\frac{{{d_2}’}}{{{d_1}}}} \right)\frac{1}{{\frac{a}{{{d_1}’}} – 1}}\)
Với d1’ –> ∞; k = 1/2.
Ảnh cùng chiều và bằng 1/2 vật. Vẽ ảnh theo các trị số tính được.
b) Ta phải có d2’ < 0 và |k| = 2
\(\begin{array}{l}
k = {k_1}{k_2};{k_1} = \frac{{{f_1}}}{{{f_1} – {d_1}}} = \frac{{20}}{{20 – {d_1}}};{k_2} = \frac{{{f_2}}}{{{f_2} – {d_2}}} = \frac{{10}}{{10 + {d_2}}}\\
{d_2} = a – {d_1}’ = 30 – \frac{{20{d_1}}}{{{d_1} – 20}} = \frac{{10{d_1} – 600}}{{{d_1} – 20}}\\
{k_2} = \frac{{10}}{{10 + \frac{{10{d_1} – 600}}{{{d_1} – 20}}}} = \frac{{10({d_1} – 20)}}{{20{d_1} – 800}} = \frac{{{d_1} – 20}}{{2({d_1} – 40)}}\\
\Rightarrow k = \frac{{10}}{{40 – {d_1}}} = \pm 2 \Rightarrow \left\{ \begin{array}{l}
{d_{11}} = 35cm \Rightarrow {d_{21}} = – \frac{{50}}{3}cm\\
{d_{12}} = 45cm \Rightarrow {d_{22}} = – 6cm
\end{array} \right.
\end{array}\)
d21: ảnh ảo; d22: ảnh thật.
Advertisements (Quảng cáo)
Vậy d = 35cm.
Bài 30.9: Cho hệ quang học như Hình 30.3 : f1 = 30 cm ; f2 = -10 cm ; O1O2 = a.
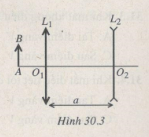
a) Cho AO1 = 36 cm, hãy :
– Xác định ảnh cuối cùng A’B’ của AB tạo bởi hệ với a = 70 cm.
– Tìm giá trị của a để A’B’ là ảnh thật.
b) Với giá trị nào của a thì số phóng đại ảnh cuối cùng A’B’ tạo bởi hệ thấu kính
không phụ thuộc vào vị trí của vật ?
\(\begin{array}{l}
AB{A_1}{B_1}A’B’\\
{d_1} = 36cm;{d_1}’ = \frac{{36.30}}{{36 – 30}} = 180cm\\
{d_2} = a – {d_1}’ = – 110cm;{d_2}’ = \frac{{( – 110)( – 10)}}{{ – 110 + 10}} = – 11cm
\end{array}\)
Ảnh ảo cách O2 11cm.
\(k = {k_1}{k_2} = \left( { – \frac{{{d_1}’}}{{{d_1}}}} \right)\left( { – \frac{{{d_2}’}}{{{d_2}}}} \right) = \frac{{180}}{{36}}.\frac{{11}}{{110}} = \frac{1}{2}\)
Ảnh cùng chiều và bằng nửa vật.
* Muốn có A’B’ thật thì:
f2 < d2 < 0 –> d2 = a – 180
Do đó:
a – 180 < 0 –> a < 180cm
a – 180 > -10 –> a > 170cm
Hay 170cm < a < 180cm
b) k = k1k2nhưng \({k_1} = \frac{{{f_1}}}{{{f_1} – d}};{k_2} = \frac{{{f_2}}}{{{f_2} – {d_2}}}\)
Mà:
\(\begin{array}{l}
{d_2} = a – {d_1}’ = a – \frac{{{d_1}{f_1}}}{{{d_1} – {f_1}}} = \frac{{(a – {f_1}){d_1}{\rm{ – a}}{{\rm{f}}_1}}}{{{d_1} – {f_1}}}\\
{f_2} – {d_2} = {f_2} – \frac{{(a – {f_1}){d_1}{\rm{ – a}}{{\rm{f}}_1}}}{{{d_1} – {f_1}}} = \frac{{({f_2} + {f_1} – a){d_1} + a{f_1} – {f_1}{f_2}}}{{{d_1} – {f_1}}}\\
{k_2} = \frac{{{f_2}({d_1} – {f_1})}}{{({f_2} + {f_1} – a){d_1} + a{f_1} – {f_1}{f_2}}}
\end{array}\)
Vậy
\(k = \frac{{{f_1}{f_2}}}{{{f_1}{f_2} – a{f_1} – ({f_2} + {f_1} – a){d_1}}}\)
Muốn k không phụ thuộc vào d1 ta phải có:
f2 + f1 – a = 0 à a = f1 + f2 (tức F1’ ≡ F2)
Chú ý: Có thể giải bằng phương pháp hình học, dùng hai tia sang tương ứng song song với trục chính.

