Câu C1: Áp dụng quy tắc nắm tay phải và quy tắc bàn tay trái, hãy chỉ ra rằng hai dòng điện song song, ngược chiều thì đẩy nhau.
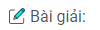
Xét hai dòng điện ngược chiều chạy trong hai dây dẫn thẳng song song như hình vẽ.
Lần lượt áp dụng các quy tắc bàn tay trái và quy tắc nắm tay phải.
Xét dòng điện I2 ở trong từ trường của dòng điện I1 ; cảm ứng từ \({\overrightarrow B _1}\) tại O2 (quy tắc nắm tay phải) hướng ra mặt phẳng tờ giấy. Áp dụng quy tắc bàn tay trái cho dòng điện I2, ta có lực từ \({\overrightarrow F _{12}}\) có hướng đẩy dòng I2 ra xa dòng I1
Lí luận tương tự cho dòng điện l1, ta cũng có lực từ \({\overrightarrow F _{21}}\) có hướng đẩy dòng l1 ra xa dòng I2
Vậy: Hai dòng điện chạy ngược chiều và song song thì đẩy nhau.
Bài 1: Chọn phương án đúng.
Khi tăng đồng thời cường độ dòng điện trong cả hai dây dẫn song song lên 3 lần thì lực tác dụng lên một đơn vị chiều dài của mỗi dây tăng lên:
A. 3 lần. B. 6 lần.
C. 9 lần. D. 12 lần.
Advertisements (Quảng cáo)
C là phương án đúng.
Bài 2: Hai dây dẫn thẳng, dài, song song với nhau và cách nhau d = 10cm đặt trong không khí. Dòng điện trong hai dây đó có cường độ là I1 = 2A, I2 = 5A. Tính lực từ tác dụng lên một đoạn có chiều dài 0,20m của mỗi dây dẫn.
Theo giả thiết r = d = 10cm = 0,1 (m);\( I\)1 = 2(A) ; \(I\)2 = 5(A).
Lực từ tác dụng lên một đoạn có chiều dài \(l = 0,2\) (m) của mỗi dây dẫn là:
Advertisements (Quảng cáo)
\(F = {2.10^{ – 7}}{{{I_1}{I_2}} \over r}l = {2.10^{ – 7}}.{{2\,.\,5} \over {0,1}}.0,2 = {4.10^{ – 6}}\left( N \right)\)
Bài 3: Hai dây dẫn thẳng, dài, song song được đặt trong không khí. Cường độ dòng diện trong hai dây dẫn đó bằng nhau và bằng I = 1A. Lực tác dụng trên mỗi đơn vị dài của mỗi dây bằng 2.10-5N. Hỏi hai dây đó cách nhau bao nhiêu?
Hai dây dẫn dài cách nhau r, đặt song song có dòng điện chạy qua I1 = I2 = 1(A). Lực tác dụng lên một đơn vị dài F = 2.10-5 (N)
Ta có: \(F = {2.10^{ – 7}}{{{I_1}{I_2}} \over r} \)
\(\Rightarrow r = {{{{2.10}^{ – 7}}.{I_1}{I_2}} \over F} = {{{{2.10}^{ – 7}}.1.1} \over {{{2.10}^{ – 5}}}} = {10^{ – 2}}\left( m \right)\)
Bài 4: Hai vòng tròn dây dẫn đặt cách nhau một khoảng rất nhỏ. Vòng dây dẫn dưới giữ cố định, vòng trên nối với một đầu đòn cân (Hình 31.2 SGK). Khi cho hai dòng điện cường độ bằng nhau vào hai vòng dây thì chúng hút nhau. Đặt thêm một quả cân khối lượng 0,1g vào đĩa cân bên kia thì cân trở lại thăng bằng và lúc đó hai vòng cách nhau 2mm. xác định cường độ dòng điện trong mỗi vòng dây? Cho biết bán kính mỗi vòng dây bằng 5cm. Lấy g = 10m/s2.
Có thể áp dụng công thức 31.1 để tính lực từ tác dụng lên mỗi vòng dây, vì hai vòng dây ở dây cách nhau một khoảng rất nhỏ.
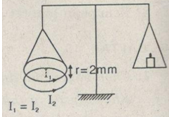
Chiều dài của mỗi vòng dây chính là chu vi đường tròn.
\(l = 2\pi R\)
Hai dòng điện cùng chiều chạy qua hai vòng dây dẫn song song thì hút nhau, sau đó cân được cân bằng khi đặt vào đĩa cân bên phải một vật khối lượng m.
Bán kính mỗi dòng dây R = 5(cm)
Ta có: \(F = {2.10^{ – 7}}{{{I_1}{I_2}} \over r}l = mg\)
\( \Rightarrow \,\,\,\,F = {2.10^{ – 7}}{{{I^2}} \over r}l = mg \Rightarrow {I^2} = {{F.r} \over {{{2.10}^{ – 7}}l}} = {{mg\,r} \over {{{2.10}^{ – 7}}l}}\)
\({I^2} = {{0,{{1.10}^{ – 3}}{{.10.2.10}^{ – 3}}} \over {{{2.10}^{ – 7}}.2\pi {{.5.10}^{ – 2}}}} = 31,85\Rightarrow I \approx 5,64\left( A \right)\)
