Bài 6: Cho bốn điểm \(A,B,C\) và \(D\) không đồng phẳng. Gọi \(M,N\) lần lượt là trung điểm của \(AC\) và \(BC\). Trên đoạn \(BD\) lấy điểm \(P\) sao cho \(BP=2PD\).
a) Tìm giao điểm của đường thẳng \(CD\) và mặt phẳng \((MNP)\).
b) Tìm giao tuyến của hai mặt phẳng \((MNP)\) và \((ACD)\).
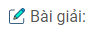
 4
4
a) Trong \((BCD)\), gọi \(I\) là giao điểm của \(NP\) và \(CD\).
\(I\in NP\subset (MNP)\) do đó \(CD\cap (MNP)=I\).
b) Trong \((ACD)\), gọi \(J=MI\cap AD\)
\(J\in AD\subset (ACD)\), \(M\in AC\subset (ACD)\)
Do đó \((MNP)\cap(ACD)=MI\).
Bài 7: Cho bốn điểm \(A, B, C\) và \(D\) không đồng phẳng. Gọi \(I,K\) lần lượt là trung điểm của hai đoạn thẳng \(AD\) và \(BC\)
a) Tìm giao tuyến của hai mặt phẳng \((IBC)\) và \((KAD)\)
b) Gọi \(M\) và \(N\) là hai điểm lần lượt lấy trên hai đoạn thẳng \(AB\) và \(AC\). Tìm giao tuyến của hai mặt phẳng \((IBC)\) và \((DMN)\).
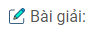
a) Chứng minh \(I, K\) là hai điểm chung của \((BIC)\) và \((AKD)\)
\(I\in AD\Rightarrow I\in(KAD)\Rightarrow I\in(KAD)\cap (IBC)\),
\(K\in BC\Rightarrow K\in(BIC)\Rightarrow K\in(KAD)\cap (IBC)\),
Hay \(KI=(KAD)\cap (IBC)\)
b) Trong \(ACD)\) gọi \(E = CI ∩ DN\Rightarrow E\in (IBC)\cap (DMN)\)
Advertisements (Quảng cáo)
Trong \((ABD)\) gọi \(F = BI ∩ DM\Rightarrow F\in (IBC)\cap (DMN)\).
Do đó \(EF=(IBC)\cap (DMN)\)
Bài 8: Cho tứ diện \(ABCD\). Gọi \(M\) và \(N\) lần lượt là trung điểm của các cạnh \(AB\) và \(CD\) trên cạnh \(AD\) lấy điểm \(P\) không trùng với trung điểm của \(AD\)
a) Gọi \(E\) là giao điểm của đường thẳng \(MP\) và đường thẳng \(BD\). Tìm giao tuyến của hai mặt phẳng \((PMN)\) và \((BCD)\)
b) Tìm giao điểm của mặt phẳng \((PMN)\) và \(BC\).
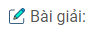
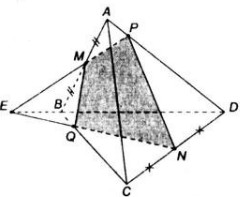
a) Ta có \(E\in BD\Rightarrow E\in(BCD)\)
\(E\in MP\Rightarrow E\in(PMN)\)
Do đó: \(E\in (BCD)\cap(PMN)\)
\(N\in CD\Rightarrow N\in(BCD)\)
\(N \in(PMN)\)
Advertisements (Quảng cáo)
Do đó: \(N\in (BCD)\cap(PMN)\)
\(=> (PMN) ⋂ (BCD) = EN\)
b) Trong mặt phẳng \((BCD)\) gọi \(Q\) là giao điểm của \(NE\) và \(BC\) thì \(Q\) là giao điểm của \((PMN)\) và \(BC\).
Bài 9: Cho hình chóp \(S.ABCD\) có đáy là hình bình hành \(ABCD\). Trong mặt phẳng đáy vẽ đường thẳng \(d\) đi qua \(A\) và không song song với các cạnh của hình bình hành, \(d\) cắt đoạn \(BC\) tại \(E\). Gọi \(C’\) là một điểm nằm trên cạnh \(SC\)
a) Tìm giao điểm \(M\) của \(CD\) và mặt phẳng \((C’AE)\)
b) Tìm thiết diện của hình chóp cắt bởi mặt phẳng \((C’AE)\)
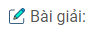
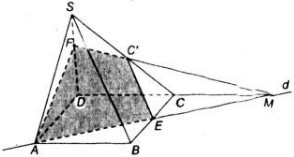
a) Trong \((ABCD)\) gọi \(M = AE ∩ DC \Rightarrow M ∈ AE\),
\(AE ⊂ ( C’AE) \Rightarrow M ∈ ( C’AE)\).
Mà \(M ∈ CD \Rightarrow M = DC ∩ (C’AE)\)
b) Trong \((SDC) : MC’ ∩ SD = F\). Do đó thiết diện là \(AEC’F\).
Bài 10: Cho hình chóp \(S. ABCD\) có \(AB\) và \(CD\) không song song. Gọi \(M\) là một điểm thuộc miền trong của tam giác \(SCD\)
a) Tìm giao điểm \(N\) của đường thẳng \(CD\) và mặt phẳng \((SBM)\)
b) Tìm giao tuyến của hai mặt phẳng \((SBM)\) và \((SAC)\)
c) Tìm giao điểm \(I\) của đường thẳng \(BM\) và mặt phẳng \((SAC)\)
d) Tìm giao điểm \(P\) của \(SC\) và mặt phẳng \((ABM)\), từ đó suy ra giao tuyến của hai mặt phẳng \((SCD)\) và \((ABM)\)
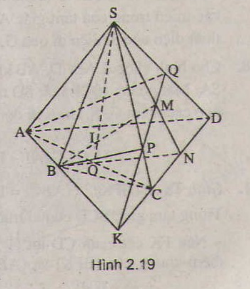
a) Trong \((SCD)\) kéo dài \(SM\) cắt \(CD\) tại \(N\). Do đó: \(N=CD\cap(SBM)\)
b) \((SBM) ≡ (SBN)\).
Trong \((ABCD)\) gọi \(O=AC\cap BN\)
Do đó: \(SO=(SAC)\cap(SBM)\).
c) Trong \((SBN)\) gọi \(I\) là giao của \(MB\) và \(SO\).
Do đó: \(I=BM\cap (SAC)\)
d) Trong \((ABCD)\) , gọi giao điểm của \(AB\) và \(CD\) là \(K\).
Trong \((SCD)\), gọi \(P= MK\cap SC\)
Do đó: \(P=SC\cap (ABM)\)
Trong \((SDC)\) gọi \(Q=MK\cap SD\)
Từ đó suy ra được giao tuyến của hai mặt phẳng \((SCD)\) và (\(ABM)\) là \(KQ\).

