Câu 1. Trong các mệnh đề sau đây, mệnh đề nào đúng ?
a. Có duy nhất một mặt phẳng đi qua ba điểm cho trước
b. Có duy nhất một mặt phẳng đi qua ba điểm không thẳng hàng cho trước
c. Ba điểm không thẳng hàng cùng thuộc một mặt phẳng duy nhất
Mệnh đề a sai vì có vô số mặt phẳng đi qua 3 điểm thẳng hàng cho trước.
Mệnh đề b, c đúng
Câu 2. Em hãy giải thích vì sao các đồ vật có bốn chân như bàn, ghế, … thường dễ bị cập kênh
Thường bốn chân của vật nằm trên một mặt phẳng, vật không cập kênh (gập ghềnh) nhưng mặt đất thường không phẳng do đó bàn ghế thường hay cập kênh.
Câu 3. Với một cái thước thẳng, làm thế nào để phát hiện một mặt bàn có phẳng hay không ? Nói rõ căn cứ vào đâu mà ta làm như vậy
Đặt thước trên bàn, đẩy thước di động. Nếu mặt bàn thật phẳng thì cạnh thước lúc nào cũng sát với mặt bàn, nếu mặt bàn không thật phẳng thì cạnh thước có lúc không sát với mặt bàn và ta trông thấy có khe hở giữa cạnh thước và mặt bàn. Căn cứ vào định lí : “Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đều nằm trong mặt phẳng đó”.
Câu 4. Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến △. Trên (P) cho đường thẳng a và trên (Q) cho đường thẳng b. Chứng minh rằng nếu a và b cắt nhau thì giao điểm phải nằm trên △
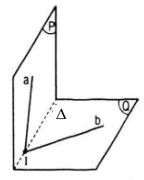
Ta có: (P) ∩ (Q) = Δ
Giả sử I = a ∩ b.
Ta có: I ϵ a mà a ⊂ (P) nên I ϵ (P)
I ϵ b mà b ⊂ (Q) nên I ϵ (Q)
Từ đó suy ra I ϵ (P) ∩ (Q) = Δ
Câu 5. Cho mặt phẳng (P) và ba điểm không thẳng hàng A, B, C cùng nằm ngoài (P). Chứng minh rằng nếu ba đường thẳng AB, BC, CA đều cắt mp (P) thì các giao điểm đó thẳng hàng
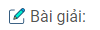
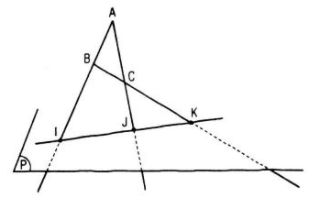
Gọi I, J, K lần lượt là giao điểm của AB, AC, BC với mp(P). A, B, C không thẳng hàng nên có mp(ABC).
Rõ ràng I, J, K ϵ mp(ABC) và I, J, K nằm trên giao tuyến của hai mặt phẳng (P) và (ABC).
Vậy I, J, K thẳng hàng.
Câu 6. Trong các mệnh đề sau đây, mệnh đề nào đúng ?
a. Có duy nhất một mặt phẳng đi qua một điểm và một đường thẳng cho trước
b. Có duy nhất một mặt phẳng đi qua một điểm và một đường thẳng chứa điểm đó
c. Có duy nhất một mặt phẳng đi qua một điểm và một đường thẳng không chứa điểm đó
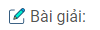
a) b) mệnh đề sai vì có vô số mặt phẳng đi qua một điểm và một đường thẳng chứa điểm đó.
Mệnh đề c đúng.
Câu 7. Hãy tìm mệnh đề đúng trong các mệnh đề sau đây:
a. Có một mặt phẳng duy nhất đi qua hai đường thẳng cho trước
b. Có một mặt phẳng duy nhất đi qua hai đường thẳng cắt nhau cho trước
c. Có duy nhất một mặt phẳng đi qua hai đường thẳng mà hai đường thẳng đó lần lượt nằm trên hai mặt phẳng cắt nhau
Advertisements (Quảng cáo)
Mệnh đề a sai vì có vô số mặt phẳng đi qua hai đường thẳng trùng nhau
Mệnh đề c sai vì không có mặt phẳng nào đi qua hai đường thẳng chéo nhau
Mệnh đề b đúng
Câu 8. Cho hai đường thẳng a và b cắt nhau. Một đường thẳng c cắt cả a và b. Có thể kết luận rằng ba đường thẳng a, b, c cùng nằm trong một mặt phẳng hay không ?
Không. Bởi vì nếu a và b cắt nhau tại I thì đường thẳng c qua I cắt cả a và b nhưng nó có thể không thuộc mp(a, b)
Câu 9. Cho ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng sao cho chúng đôi một cắt nhau. Chứng minh rằng chúng đồng quy
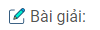
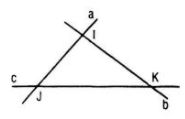
Gọi I = a ∩ b; J = a ∩ c, K = b ∩ c.
Nếu các điểm I, J, K phân biệt từng cặp thì a, b, c cùng thuộc mp(IJK), trái với giả thiết.
Vậy I, J, K trùng nhau do đó a, b, c đồng quy.
Câu 10. Cho hai đường thẳng a và b cắt nhau tại điểm O và đường thẳng c cắt mp(a , b) ở điểm I khác O. Gọi M là điểm di động trên c và khác I. Chứng minh rằng giao tuyến của các mặt phẳng (M , a), (M , b) nằm trên một mặt phẳng cố định
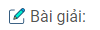
Ta có: \(M \in \left( {M,a} \right) \cap \left( {M,b} \right)\)
Vì \(O = a \cap b\) nên \(O \in \left( {M,a} \right) \cap \left( {M,b} \right) \)
\(\Rightarrow \left( {M,a} \right) \cap \left( {M,b} \right) = MO\)
Vì M \(\in\) c nên MO ⊂ mp(O, c)
Vậy giao tuyến của hai mặt phẳng (M, a), (M, b) nằm trên mặt phẳng (O, c) cố định.
Câu 11. Cho hình bình hành ABCD nằm trong mặt phẳng (P) và một điểm S nằm ngoài mp(P). Gọi M là điểm nằm giữa S và A ; N là điểm giữa S và B; giao điểm của hai đường thẳng AC và BD là O
a. Tìm giao điểm của mặt phẳng (CMN) với đường thẳng SO
b. Xác định giao tuyến của hai mặt phẳng (SAD) và (CMN)
Advertisements (Quảng cáo)
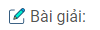
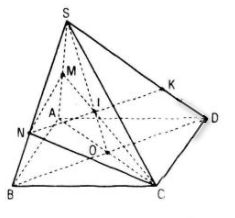
a. Tìm SO ∩ (CNM)
Trong mặt phẳng (SAC) gọi I là giao điểm của SO với CM : I = SO ∩ CM
mà CM ⊂ (CMN) nên I = SO ∩ (CMN)
b. Tìm (SAD) ∩ (CMN)
Trong mp(SBD) gọi K là giao điểm của NI và SD: K = NI ∩ SD
Ta có: M, K \(\in\) (CMN) và M, K \(\in\) (SAD)
Do đó (SAD) ∩ (CMN) = MK
Câu 12. Vẽ một số hình biểu diễn của một hình chóp tứ giác trong các trường hợp đáy là tứ giác lồi, đáy là hình bình hành, đáy là hình thang
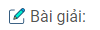
Nếu đáy của hình chóp là tứ giác lồi tùy ý, ta có hình thường dùng là hình a hoặc hình b
Nếu đáy của hình chóp tứ giác là hình bình hành, hình chữ nhật, hình thoi hay hình vuông, ta có hình biểu diễn thường dùng của hình chóp là hình c
Nếu đáy của hình chóp tứ giác là hình thang ABCD (AB // CD) thì ta có hình biểu diễn thường dùng là hình d hoặc hình e.
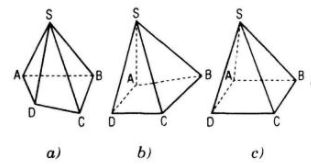
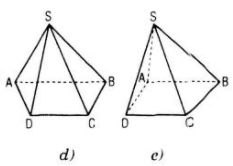
Câu 13. Thiết diện của một hình tứ diện có thể là tam giác, tứ giác hoặc ngũ giác hay không ?
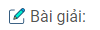
Thiết diện của một hình tứ diện là một tam giác khi mặt phẳng cắt ba mặt tứ diện. Thiết diện là một tứ giác khi mặt phẳng cắt bốn mặt hình tứ diện. Thiết diện của một hình tứ diện không thể là một ngũ giác vì ngũ giác có năm cạnh mà tứ diện chỉ có bốn mặt.
Câu 14. Dùng bìa cứng cắt và dán lại để thành
a. Một tứ diện đều
b. Một hình chóp tứ giác có đáy là hình vuông và các mặt bên là các tam giác đều
Cắt theo mẫu sau :
Câu 15. Cho hình chóp tứ giác S.ABCD. Ba điểm A’, B’, C’ lần lượt nằm trên ba cạnh SA, SB, SC nhưng không trùng với S, A, B, C. Xác định thiết diện của hình chóp khi cắt bởi mp(A’B’C’)
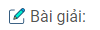
Gọi O = AC ∩ BD; O’ = A’C’ ∩ SO ; D’ = B’O’ ∩ SD
Nếu D’ thuộc đoạn SD thì thiết diện là tứ giác A’B’C’D’
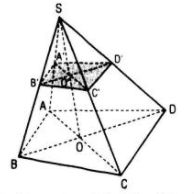
Nếu D’ nằm trên phần kéo dài của cạnh SD, ta gọi E là giao điểm của CD và C’D’, F là giao điểm của AD và A’D’
Khi ấy thiết diện là ngũ giác A’B’C’EF.
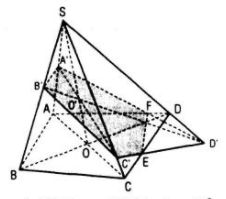
Câu 16. Cho hình chóp S.ABCD. Gọi M là một điểm nằm trong tam giác SCD
a. Tìm giao tuyến của hai mặt phẳng (SMB) và (SAC)
b. Tìm giao điểm của đường thẳng BM và mp(SAC)
c. Xác định thiết diện của hình chóp khi cắt bởi mp(ABM)
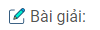
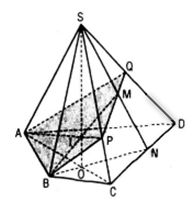
a. Tìm (SBM) ∩ (SAC)
Trong ΔSCD gọi N = SM ∩ CD
Trong mp(ABCD) gọi O = BN ∩ AC
Ta có: SO = (SBM) ∩ (SAC)
b. Tìm BM ∩ (SAC)
Chọn mặt phẳng phụ chứa BM là (SBN)
(SBN) ∩ (SAC) = SO
Gọi I = SO ∩ BM thì I = BM ∩ (SAC)
c. Trong mp(SAC) gọi P = AI ∩ SC
Trong mp(SCD), PM cắt SD tại Q.
Thiết diện của hình chóp khi cắt bởi mp(ABM) là tứ giác ABPQ.

