Bài 2.41: Cho hình hộp ABCD.A’B’C’D’. Hai điểm M và N lần lượt nằm trên hai cạnhAD và CC’ sao cho \({{AM} \over {M{\rm{D}}}} = {{CN} \over {NC’}}\).
a) Chứng minh rằng đường thẳng MN song song với mặt phẳng (ACB’)
b) Xác định thiết diện của hình hộp cắt bởi mặt phẳng đi qua MN và song song với mặt phẳng (ACB’)
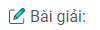
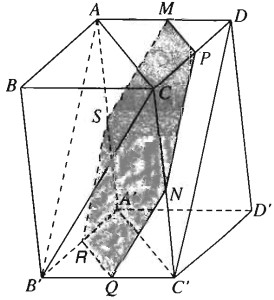
a) Vẽ MP song song với AC và cắt CD tại P
Ta có: \({{AM} \over {M{\rm{D}}}} = {{CP} \over {P{\rm{D}}}} = {{CN} \over {NC’}}\)
Do đó \(PN\parallel DC’\parallel AB’\)
Đường thẳng MN thuộc mặt phẳng (MNP) và mặt phẳng này có \(MP\parallel AC\) và \(PN\parallel AB’\). Vậy mặt phẳng(MNP) song song với mặt phẳng (ACB’) và do đó \(MN\parallel \left( {ACB’} \right)\)
b) Vì mặt phẳng (MNP) song song với mặt phẳng (ACB’) nên hai mặt phẳng đó cắt các mặt bên của hình hộp theo các giao tuyến song song.
Ta vẽ \(NQ\parallel CB’,QR\parallel C’A'(\left( {\parallel CA} \right),RS\parallel AB’\left( {\parallel PN} \right)\) và tất nhiên \(SM\parallel QN\). Thiết diện của hình hộp cắt bởi mặt phẳng đi qua MN và song song với mặt phẳng (ACB’) là hình lục giác MPNQRS có các cạnh đối diện song song với nhau từng đôi một: \(MP\parallel RQ,PN\parallel SR,NQ\parallel MS\).
Bài 2.42: Cho hình lăng trụ tứ giác ABCD.A’B’C’D’.
Advertisements (Quảng cáo)
a) Chứng minh rằng hai đường chéo AC’ và A’C cắt nhau và hai đường chéo BD’ và B’Dcắt nhau.
b) Cho E và F lần lượt là trung điểm của hai đường chéo AC và BD.Chứng minh MN = EF.
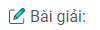
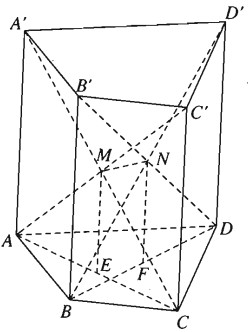
Hình bình hành ACC’A có hai đường chéo là
AC’ và A’C cắt nhau tại trung điểm Mcủa mỗi đường. Tương tự, hai đường chéo BD’ và B’D cắt nhau tại trung điểm N của mỗi đường.
b) Trung điểm E của AC là hình chiếu của trung điểm M của AC’ thep phương của cạnh lăng trụ. Tương tự, trung điểm F là hình chiếu trung điểm N của đường chéo BD’ trên BD. Ta có \(EM\parallel CC’\) và \(EM = {{CC’} \over 2}\)
Mặt khác \(FN\parallel DD’\) và \(FN = {{DD’} \over 2}\). Từ đó suy ra tứ giác MNFE là hình bình hành và ta có MN = EF.
Advertisements (Quảng cáo)
Bài 2.43: Cho hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) cắt nhau theo giao tuyến m. Trên đường thẳng d cắt \(\left( \alpha \right)\) ở A và cắt \(\left( \beta \right)\) ở B ta lấy hai diểm cố định S1,S2 không thuộc \(\left( \alpha \right)\), \(\left( \beta \right)\). Gọi M là một điểm di động trên \(\left( \beta \right)\). Giả sử các đường thẳng \(M{S_1},M{S_2}\) cắt \(\left( \alpha \right)\) lần lượt tại M1 và M2.
a) Chứng minh rằng M1M2 luôn luôn đi qua một điểm cố định.
b) Giả sử đường thẳng M1M2 cắt giao tuyến m tại K. Chứng minh rằng ba điểm K, B, M thẳng hàng.
c) Gọi b là một đường thẳng thuộc mặt phẳng \(\left( \beta \right)\) nhưng không đi qua điểm B và cắt m tại I. Chứng minh rằng khi M di động trên b thì các điểm M1 và M2 di động trên hai đường thẳng cố định thuộc mặt phẳng \(\left( \alpha \right)\).
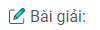
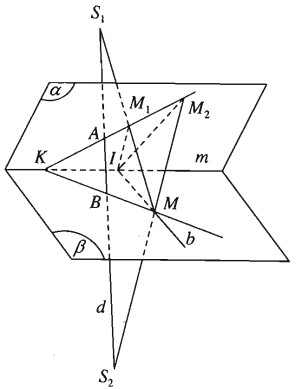
a) Mặt phẳng (M, d) cắt \(\left( \alpha \right)\) theo giao tuyến M1M2. Điểm A cũng thuộc giao tuyến đó. Vậy đường thẳng M1M2 luôn luôn đi qua điểm A cố định.
b) Mặt phẳng (M, d) cắt \(\left( \beta \right)\) theo giao tuyến BM. Điểm K thuộc giao tuyến đó nên ba điểm K, B, M thẳng hàng.
c) Giả sử b cắt m tại I thì mặt phẳng (S1, b) luôn luôn cắt \(\left( \alpha \right)\) theo giao tuyến IM1. Do đó điểm M1 di động trên giao tuyến của IM1 cố định. Còn khi M di động trên b thì mặt phẳng (S2, b) cắt \(\left( \alpha \right)\) theo giao tuyến IM2. Do đó điểm M2 chạy trên giao tuyến IM2 cố định.
Bài 2.44: Cho hình lập phương ABCD.A’B’C’D’ các trung điểm E, F của các cạnh AB, DD’. Hãy xác định các thiết diện của hình lập phương cắt bởi các mặt phẳng (EFB), (EFC), (EFC’) và (EFK) với K là trung điểm của cạnh B’C’.

Ta xác định thiết diện của hình lập phương cắt bởi các mặt phẳng sau:
– Mặt phẳng (EFB): ta vẽ \(FG\parallel AB\) và được thiết diện là hình chữ nhật ABGF, G là trung điểm của CC’.
– (h.2.67) Mặt phẳng (EFC): Nối FC và vẽ \(EG\parallel FC\), ta được thiết diện là hình thang \(ECFG\left( {AG = {1 \over 4}AA’} \right)\).
– (h.2.68) Mặt phẳng (EFC’): Nối FC’ và vẽ \(EG\parallel FC’\). Nối GC’ và vẽ \(FH\parallel GC’\). Ta được thiết diện là hình ngũ giác EGC’FH.
\(\left( {BG = {1 \over 4}BB’,AH = {1 \over 3}A{\rm{D}}} \right)\)
– (h.2.69) Mặt phẳng (EFK) với K là trung điểm của đoạn B’C’. Lấy trung điểm E’ của đoạn A’B’. Ta có \(I = EF \cap E’D’\). Ta có IK là giao tuyến của hai mặt phẳng (EFK) và (A’B’C’D’). Gọi \(G = IK \cap C’D’\). Nối F với G, vẽ \(EH\parallel FG\). Nối K với H, vẽ \(FL\parallel KH\) và nối L với E. Ta được thiết diện là hình lục giác đều EHKGFL. (G, H, L theo thứ tự là trung điểm của D’C’, B’B, AD).

