Bài 1: Cho tứ diện \(ABCD\). Gọi \(P, Q, R, S\) là bốn điểm lần lượt lấy trên bốn cạnh \(AB, BC, CD, DA\). Chứng minh rằng nếu bốn điểm \(P, Q, R, S\) đồng phẳng thì
a) Ba đường thẳng \(PQ, SR, AC\) hoặc song song hoặc đồng quy
b) Ba đường thẳng \(PS, RQ, BD\) hoặc song song hặc đồng quy
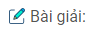
a) Gọi mặt phẳng qua bốn điểm \(P, Q, R, S\) là \((α)\). Ba mặt phẳng \(( α)\), \((ABC)\) và \((ACD)\) đôi một cắt nhau theo các giao tuyến là \(PQ, AC, RS => PQ, AC, RS\) hoặc đôi một song song hoặc đồng quy
b) Chứng minh tương tự ta được ba đường thẳng \(PS, RQ\), và \(BD\) hoặc song song hoặc đồng quy
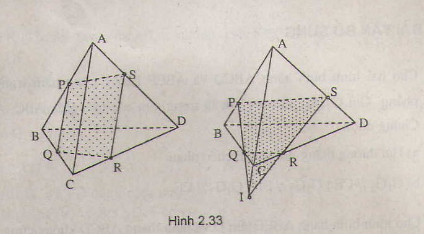
Bài 2: Cho tứ diện \(ABCD\) và ba điểm \(P, Q, R\) lần lượt trên ba cạnh \(AB, CD, BC\). Tìm giao điểm \(S\) của \(AD\) và mặt phẳng \((PQR)\) trong hai trường hợp sau đây.
a) \(PR\) song song với \(AC\)
b) \(PR\) cắt \(AC\)
Advertisements (Quảng cáo)
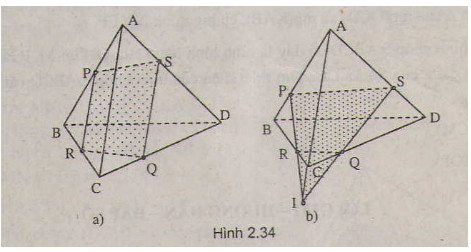
a) Nếu \(PR // CA\) thì \(( PRQ) ∩ (ACD) = QS // CA ( S ∈ AD)\) (h.2.34)
b) Nếu \(PR ∩ AC = I\) thì trong \((ACD)\) kéo dài \(IQ\) cắt \(AD\) tại \(S\) ( h..2.34 b)
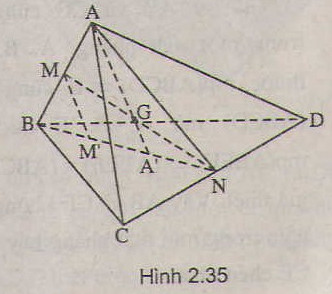
Bài 3: Cho tứ diện \(ABCD\). Gọi \(M, N\) lần lượt là trung đểm của các cạnh \(AB, CD\) và \(G\) là trung điểm của đoạn \(MN\)
a) Tìm giao điểm \(A’\) của đường thẳng \(AG\) và mặt phẳng \((BCD)\)
b) Qua \(M\) kẻ đường thẳng \(Mx\) song song với \(AA’\) và \(Mx\) cắt \((BCD)\) tại \(M’\). Chứng minh \(B, M’, A’\) thẳng hàng và \(BM’ = M’A’ = A’N\).
c) Chứng minh \(GA = 3 GA’\).
Advertisements (Quảng cáo)
a) Trong \((ABN)\): Gọi \(A’=AG \cap BN\)
suy ra \( A’ \in BN\), \(BN \subset (BCD)\).
Do đó: \(A’ \in (BCD)\) \(=> A’ = AG \cap (BCD)\).
b) \(MM’//AA’\) mà \(AA’\subset (ABA’)\) do đó: \(MM’\subset (ABA’)\)
Mặt khác \(M’\in (BCD)\) nên \(M’\) thuộc giao tuyến \(A’B\) của \((ABA’)\) và \((DBC)\)
*) Xét tam giác \(NMM’\) có:
+) \(G\) là trung điểm của \(NM\).
+) \(GA’//MM’\)
\(\Rightarrow A’\) là trung điểm của \(NM’\)
Xét tam giác \(BAA’\) có:
+) \(M \) là trung điểm của \(AB\)
+) \(MM’//AA’\)
\(\Rightarrow M’\) là trung điểm của \(BA’\)
Do đó: \(BM’=M’A’=A’N\).
c) Ta có \(GA’={1\over 2} MM’\)
\(MM’={1\over 2} AA’\)
\(\Rightarrow GA’={1\over 4} AA’\Rightarrow GA=3 GA’\)