Bài 4: Tìm mệnh đề đúng trong các mệnh đề sau:
(A) Nếu hai mặt phẳng \((α), (β)\) song song với nhau thì mọi đường thẳng nằm trong \((α)\) đều song song với \((β)\).
(B) Nếu hai mặt phẳng \((α), (β)\) song song với nhau thì mọi đường thẳng nằm trong \((α)\) đều song song với mọi đường thẳng nằm trong \((β)\).
(C) Nếu hai đường thẳng song song với nhau lần lượt nằm trong hai măt phẳng phân biệt \((α), (β)\) thì \((α), (β)\) song song với nhau
(D) Qua một điểm nằm ngoài mặt phẳng cho trước ta vẽ được một và chỉ một đường thẳng song song với mặt phẳng cho trước đó.
 A
A
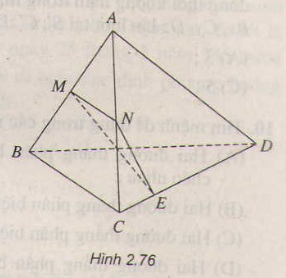
Bài 5: Cho tứ diện \(ABCD\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AB\) và \(AC\) (h.2.76), \(E\) là điểm trên cạnh \(CD\) với \(ED = 3EC\). Thiết diện tạo bởi mặt phẳng \((MNE)\) và tứ diện \(ABCD\) là:
(A) Tam giác \(MNE\)
(B) Tứ giác \(MNEF\) với \(F\) à điểm bất kì trên cạnh \(BD\)
(C) Hình bình hành \(MNEF\) với \(F\) là điểm trên cạnh \(BD\) mà \(EF // BC\).
(D) Hình thang \(MNEF\) với \(F\) là điểm trên cạnh \(BD\) mà \(EF // BC\).
\(MN//BC\) do đó \(MN//(BCD)\) nên \((BCD)\cap(MNE)\) theo giao tuyến qua \(E\) và song song với \(BC\).
Đáp án là: D
Advertisements (Quảng cáo)
Bài 6: Cho hình lăng trụ tam giác \(ABC.A’B’C’\), Gọi \(I, J\) lần lượt là trọng tâm của tam giác \(ABC\) và \(A’B’C’\) (h.2.77). Thiết diện tạo bởi mặt phẳng \((AIJ)\) với hình lăng trụ đã cho là
(A) Tam giác cân
(B) Tam giác vuông
(C) Hình thang
(D) Hình bình hành
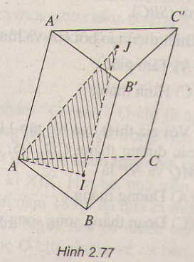
Gọi \(M,M’\) lần lượt là trung điểm của \(BC,B’C’\) do đó thiết diện là hình bình hành \(AA’M’M\).
 D
D
Advertisements (Quảng cáo)
Bài 7: Cho tứ diện \(SABC\) cạnh bằng \(a\). Gọi \(I\) là trung điểm của đoạn \(AB\), \(M\) là điểm di động trên đoạn \(AI\). Qua \(M\) vẽ mặt phẳng \((α)\) song song với \((SIC)\).
Thiết diện tạo bởi \((α)\) và tứ diện \(SABC\) là:
(A) Tam giác cân tại \(M\)
(B) Tam giác đều
(C) Hình bình hành
(D) Hình thoi
Giải
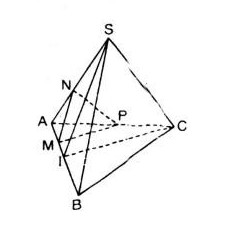
Ta có: \(IS=IC\Rightarrow MN=MP\). Do đó tam giác \(MNP\) cân tại \(M\).
 A
A
Bài 8: Với giả thiết của bài tập 7, chu vi của thiết diện tính theo \(AM = x\) là:
(A) \(x( 1 + \sqrt3)\)
(B) \(2x ( 1 + \sqrt3)\)
(C) \(3x ( 1 + \sqrt 3)\)
(D) Không tính được
Giải
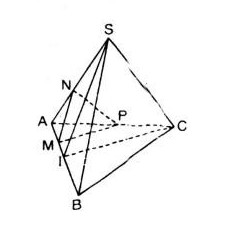
\(AM=x\Rightarrow AB=4x\Rightarrow IC=2\sqrt3x\)
\(\Rightarrow MN=MP=x\sqrt3\)
Chu vi tam giác \(MNP\) là: \(NP+MN+MP=2x+x\sqrt3+x\sqrt3\)
\(=2x(1+\sqrt3)\)
Đáp án là : B

