Bài 9: Cho hình bình hành \(ABCD\). Gọi \(Bx, Cy, Dz\) là các nửa đường thẳng song song với nhau lần lượt đi qua \(B, C, D\) và nằm về một phía của mặt phẳng \((ABCD)\) đồng thời không nằm trong mặt phẳng \((ABCD)\). Một mặt phẳng đi qua \(A\) và cắt \(Bx, Cy, Dz\) lần lượt tại \(B’, C’, D’\) với \(BB’=2, DD’=4\). Khi đó \(CC’\) bằng:
(A) 3
(B) 4
(C) 5
(D) 6
Giải
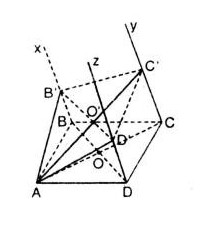
Gọi \(O,O’\) lần lượt là tâm của hình bình hành \(ABCD ,AB’C’D’\).
Ta có: \(BB’+DD’=2OO’=CC’\)
\(\Rightarrow CC’=6\)
Đáp án là D
logiaihay.com
Advertisements (Quảng cáo)
Bài 10: Tìm mệnh đề đúng trong các mệnh đề sau:
(A) Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì không chéo nhau
(B) Hai đường thẳng phân biệt không cắt nhau thì chéo nhau
(C) Hai đường thẳng phân biệt không song song thì chéo nhau
(D) Hai đường thẳng phân biệt lần lượt thuộc hai mặt phẳng khác nhau thì chéo nhau
Đáp án là: A
Advertisements (Quảng cáo)
Bài 11: Cho hình vuông \(ABCD\) và tam giác đều \(SAB\) nằm trong hai mặt phẳng khác nhau. Gọi \(M\) là điểm di động trên đoạn \(AB\). Qua \(M\) vẽ mặt phẳng \((\alpha)\) song song với \((SBC)\)
Thiết diện tạo bởi \((\alpha)\) và hình chóp \(S.ABCD\) là hình gì?
(A) Tam giác
(B) Hình bình hành
(C) Hình thang
(D) Hình vuông
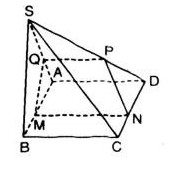
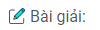 C
C
Bài 12: Với giả thiết của bài tập 11, gọi \(N, P, Q\) lần lượt là giao của mặt phẳng \((\alpha)\) với các đường thẳng \(CD, DS, SA\). Tập hợp các giao điểm \(I\) của hai đường thẳng \(MQ\) và \(NP\) là:
(A) Đường thẳng
(B) Nửa đường thẳng
(C) Đoạn thẳng song song với \(AB\)
(D) Tập hợp rỗng
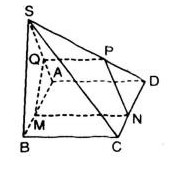
\(MQ\subset (SAB)\), \(NP\subset(SCD)\)
\(\Rightarrow I\in(SAB)\cap(SCD)\).
 C
C

