Bài 2.32: Hình chiếu so H ng song của hai đường thẳng chéo nhau có thể song song với nhau hay không? Hình chiếu song song của hai đường thẳng cắt nhau có song song với nhau hay không?
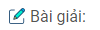
Giả sử a và b là hai đường thẳng chéo nhau có hình chiếu là a’ và b’. Nếu mặt phẳng (a, a’) và mặt phẳng (b, b’) song song với nhau thì \(a’\parallel b’\). Vậy hình chiếu song song của hai đường thẳng chéo nhau có thể song song.
Nếu a và b là hai đường thẳng cắt nhau tại O và hình chiếu của O là O’ thì \(O’ \in a’\) và \(O’ \in b’\) tức là a’ và b’ có điểm chung. Vậy hình chiếu song song của hai đường thẳng cắt nhau không thể song song được.
Bài 2.33: Trong mặt phẳng \(\left( \alpha \right)\) cho một tam giác ABC bất kì. Chứng minh rằng có thể xem tam giác ABC là hình chiếu song song của một tam giác đều nào đó.
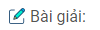
Cho tam giác ABC bất kì nằm trong mặt phẳng \(\left( \alpha \right)\). Gọi \(\left( \beta \right)\) là mặt phẳng qua BC và khác với \(\left( \alpha \right)\). Trong \(\left( \beta \right)\) ta vẽ tam giác đều BCD. Vậy ta có thể xem tam giác ABC cho trước là hình chiếu song song của tam giác đều DBC theo phương chiếu DA lên mặt phẳng \(\left( \alpha \right)\).
Advertisements (Quảng cáo)
Bài 2.34: Vẽ hình biểu diễn của một hình lục giác đều.
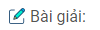
Với hình lục giác đều ABCDEF ta nhận thấy:
– Tứ giác OABC là hình bình hành ( vừa là hình thoi);
Advertisements (Quảng cáo)
– Các điểm D, E, F lần lượt là các điểm đối xứng của các điểm A, B, C qua tâm O
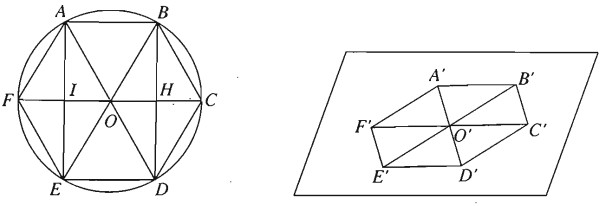
Từ đó suy ra cách vẽ hình biểu diễn của lục giác đều ABCDEF như sau: (h.2.54)
– Vẽ hình bình hành O’A’B’C’ biểu diễn cho hình bình hành OABC..
– Lấy các điểm D’, E’, F’ lần lượt đối xứng của A’, B’, C’ qua tâm O’, ta được hình biểu diễn A’B’C’D’E’F’ của hình lục giác đều ABCDEF.
Chú ý. Ta có thể vẽ hình biểu diễn hình lục giác đều dựa trên sự phân tích sau đây ở hình thực ABCDEF (h.2.53) :
– Tứ giác ABDE là hình chữ nhật;
– Gọi I là trung điểm của cạnh AE và H là trung điểm của cạnh BD;
– Các điểm F và C đối xứng của O lần lượt qua I và H.
Từ đó ta có cách vẽ sau đây:
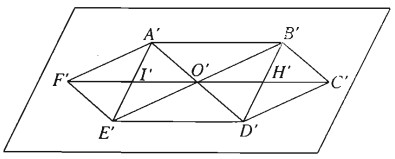
– Vẽ hình bình hành A’B’D’E’ biểu diễn cho hình chữ nhật ABDE
– Gọi I’ và H’ lần lượt là trung điểm của A’E’và B’D’.
– Gọi F’ đối xứng với O’ qua I’ và C’ đối xứng với O’ qua H’, ta được hình biểu diễn A’B’C’D’E’F’ của hình lục giác đều.

