Bài 1: Tìm mệnh đề sai trong các mệnh đề sau đây:
(A) Nếu hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác nữa
(B) Nếu hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì chúng song song với nhau
(C) Nếu hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau
(D) Nếu một đường thẳng cắt một trong hai mặt phẳng song song với nhau thì sẽ cắt mặt phẳng còn lại
Đáp án là : C.
Bài 2: Nếu ba đường thẳng không cùng nằm trong một mặt phẳng và đôi một cắt nhau thì ba đường thẳng đó
(A) Đồng quy
(B) Tạo thành tam giác
(C) Trùng nhau
(D) Cùng song song với một mặt phẳng
Đáp án là : A
Advertisements (Quảng cáo)
Bài 3: Cho tứ diện \(ABCD\). Gọi \(I, J\) và \(K\) lần lượt là trung điểm của \(AC, BC\) và \(BD\) (h.2.75). Giao tuyến của hai mặt phẳng \((ABD)\) và \((IJK)\) là
(A) \(KD\)
(B) \(KI\)
(C) Đường thẳng qua \(K\) và song song với \(AB\)
(D) Không có
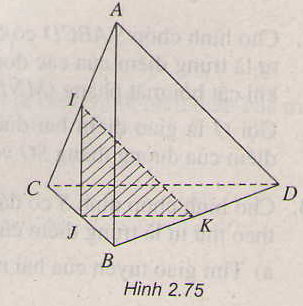
Đáp án : C
Advertisements (Quảng cáo)
Bài 4: Cho hình bình hành \(ABCD\). Qua \(A, B, C, D\) lần lượt vẽ bốn nửa đường thẳng \(Ax, By, Cz, Dt\) ở cùng phía đối với mặt phẳng \((ABCD)\), song song với nhau và không nằm trong mặt phẳng \((ABCD)\). Một mặt phẳng \((β)\) lần lượt cắt \(Ax, By, Cz\) và \(Dt\) tại \(A’, B’, C’\) và \(D’\).
a) Chứng minh mặt phẳng \((Ax, By)\) song song với mặt phẳng \(( Cz, Dt)\)
b) Gọi \(I = AC ∩ BD, J = A’C’ ∩ B’D’\). Chứng minh \(IJ\) song song với \(AA’\)
c) Cho \(AA’ = a, BB’ = b, CC’ = c\). Hãy tính \(DD’\).
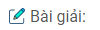
a) \(Ax // Dt\) (giả thiết) và \(AB // CD\) (vì \(ABCD\) là hình bình hành).
Do đó \((Ax, By) // ( Cz, Dt)\)
b) Ta có \((Ax, By) // ( Cz, Dt)\). Mặt phẳng \((A’B’C’D’)\) lần lượt cắt hai mặt phẳng \((Ax, By)\) và \(( Cz, Dt)\) theo giao tuyến \(A’B’\) và \(C’D’\) do đó \(A’B’//C’D’\).
Tương tự ta chứng minh được: \(A’D’//B’C’\)
Do đó \(A’B’C’D’\) là hình bình hành.
\(J=A’C’\cap B’D’\) nên \(J\) là trung điểm của \(A’C’\)
Suy ra \(IJ\) là đường trung bình hình thang \(A’C’CA\) do đó \(Ị\) song song với \(AA’\).
c) Theo tính chất của đường trung bình hình thang ta có:
\(AA’+CC’=2IJ\)
\(BB’+DD’=2IJ\)
Do đó : \(DD’=AA’+CC’-BB’\)
\(DD’ = a + c – b\).

