Bài 28: Xác định mỗi tập hợp số sau và biểu diễn nó trên trục số
a) \(( – 3;3) \cup ( – 1;0)\)
b) \(( – \infty ;0) \cup (0;1)\)
c) \(( – 1;3) \cup {\rm{[0}};5{\rm{]}}\)
d) \(( – 2;2{\rm{]}} \cup {\rm{[}}1;3)\)

a) \(( – 3;3) \cup ( – 1;0) = ( – 3;3)\)
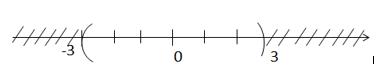
b) \(( – 1;3) \cup {\rm{[0}};5{\rm{] = ( – 1;5]}}\)
Advertisements (Quảng cáo)

c) \(( – \infty ;0) \cup (0;1) = \emptyset \)
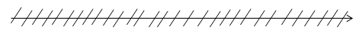
d) \(( – 2;2{\rm{]}} \cup {\rm{[}}1;3) = {\rm{[}}1;2]\)
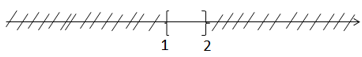
Advertisements (Quảng cáo)
Bài 29: Cho \(a,b \in R,a < b\). Hãy xét quan hệ bào hàm \( \subset \) của các tập hợp sau:
a) \(A = {\rm{[}}a;b{\rm{]}}\)
b) \(B = (a;b{\rm{]}}\)
c) \(C = {\rm{[}}a;b)\)
d) \(D = (a;b)\)

\(B \subset A,C \subset A,D \subset A,D \subset B,D \subset C\)
Bài 30: Xác định tập hợp \(A \cap B\), với:
a) \(A = {\rm{[1;5]; B = ( – 3;2)}} \cup {\rm{(3;7);}}\)
b) \(A = ( – 5;0) \cup {\rm{ (3;5);B = ( – 1;2)}} \cup {\rm{(4;6)}}{\rm{.}}\)

a) \(A \cap B = {\rm{[}}1;2) \cup (3;5]\)
b) \(A \cap B = ( – 1;0) \cup (4;5)\)

