Bài 5: Xem các bài giải sau đây và cho biết mỗi bài giải đó đúng hay sai? Vì sao?
a)
\({{(x – 2)(x – 1)} \over {\sqrt x – 1}} = 0 \)
\(\Leftrightarrow {{x – 2} \over {\sqrt x – 1}}(x – 1) = 0 \)
\(\Leftrightarrow \left[ \matrix{
{{x – 1} \over {\sqrt x – 1}} = 0 \hfill \cr
x – 1 = 0 \hfill \cr} \right.\)
Ta có: \({{x – 2} \over {\sqrt x – 1}} = 0 \Leftrightarrow x = 2;\,x – 1 = 0 \Leftrightarrow x = 1\)
Vậy tập nghiệm của phương trình đã cho là S = {1, 2}
b)
\(\eqalign{
& \sqrt {{x^2} – 2} = 1 – x \Leftrightarrow {x^2} – 2 = {(1 – x)^2} \cr
& \Leftrightarrow {x^2} – 2 = 1 – 2x + {x^2} \Leftrightarrow 2x = 3 \Leftrightarrow x = {3 \over 2} \cr} \)
Vậy phương trình có nghệm: \(x = {3 \over 2}\)

a) Sai khi kết luận tập nghiệm:
\(x = 1\) không thuộc ĐKXĐ của phương trình
b) Sai vì khi bình thường hai vế chỉ được phương trình hệ quả
Nhất thiết phải thử lại giá trị x tìm được.
Bài 6: Giải và biện luận các phương trình
a) \((m^2 + 2)x – 2m = x – 3\)
b) \(m(x – m) = x + m – 2\)
c) \(m(x – m + 3) = m(x – 2) + 6\)
d) \(m^2(x – 1) + m = x(3m – 2)\)

Advertisements (Quảng cáo)
a) Ta có:
\((m^2 + 2)x – 2m = x – 3 ⇔ (m^2+ 1)x = 2m – 3\)
Vì \(m^2+ 1 ≠ 0; ∀m\) nên phương trình có nghiệm duy nhất \(x = {{2m + 3} \over {{m^2} + 1}}\)
b) \(m(x – m) = x + m – 2 \)
\(⇔ mx – x =m^2+ m – 2\)
\( ⇔ (m – 1)x = (m – 1)(m + 2)\)
+ Nếu \(m ≠ 1\) thì phương trình có nghiệm duy nhất: \(x = {{(m – 1)(m + 2)} \over {m – 1}} = m + 2\)
+ Nếu \(m = 1\) thì \(0x = 0\), phương trình có tập nghiệm là \(S =\mathbb R\)
c) \(m(x – m + 3) = m(x – 2) + 6 \)
\(⇔ mx – {m^2}+ 3m = mx – 2m + 6\)
\(⇔ 0x = {m^2}– 5m + 6 ⇔ 0x = (m – 2)( m – 3)\)
+ Nếu \(m =2\) hoặc \(m = 3\) thì phương trình có tập nghiệm là \(S =\mathbb R\)
+ Nếu \(m ≠ 2\) và \(m ≠ 3\) thì phương trình vô nghiệm.
Advertisements (Quảng cáo)
d) \({m^2}(x – 1) + m = x(3m – 2) \)
\(⇔ {m^2}x – {m^2}+ m = (3m – 2)x\)
\(⇔ ( {m^2}– 3m + 2)x = {m^2}– m \)
\(⇔ (m – 1)(m – 2)x = m(m – 1)\)
+ Nếu \(m ≠ 1\) và \(m ≠ 2\) thì phương trình có nghiệm duy nhất: \(x = {{m(m – 1)} \over {(m – 1)(m – 2)}} = {m \over {m – 2}}\)
+ Nếu \(m = 1\), ta có: \(0x = 0\), phương trình tập nghiệm \(S =\mathbb R\)
+ Nếu \(m = 2\), ta có \(0x = 2\), phương trình vô nghiệm \(S = Ø \)
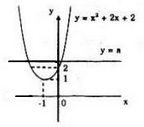
Bài 7: Dựa vào hình bên, tìm các giá trị của a để phương trình: \(3x + 2 = – {x^2} + x + a\) có nghiệm dương.
Khi đó, hãy tìm nghiệm dương của phương trình.

Ta có:
\(3x{\rm{ }} + {\rm{ }}2= {\rm{ }} – {x^2} + {\rm{ }}x{\rm{ }} + {\rm{ }}a{\rm{ }} \Leftrightarrow {\rm{ }}{x^2} + {\rm{ }}2x{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}a\)
Nghiệm của phương trình là hoành độ giao điểm của (P): \(x^2+ 2x + 2\) và đường thẳng d: \(y = a\)
Dựa vào đồ thị ta có:
Phương trình có nghiệm dương khi và chỉ khi \(a > 2\), khi đó nghiệm dương của phương trình là \(x = – 1 + \sqrt {a – 1} \)
Bài 8: Giải và biện luận các phương trình
a) \(\left( {m{\rm{ }} – {\rm{ }}1} \right){x^2} + {\rm{ }}3x{\rm{ }} – {\rm{ }}1{\rm{ }} = {\rm{ }}0\)
b) \({x^2} – {\rm{ }}4x{\rm{ }} + {\rm{ }}m{\rm{ }} – {\rm{ }}3{\rm{ }} = {\rm{ }}0\)

a) \(\left( {m{\rm{ }} – {\rm{ }}1} \right){x^2} + {\rm{ }}3x{\rm{ }} – {\rm{ }}1{\rm{ }} = {\rm{ }}0\)
+ Với \(m = 1\), phương trình trở thành: \(3x – 1 = 0 \Leftrightarrow x = {1 \over 3}\)
+ Với \(m ≠ 1\), ta có: \(Δ = 9 + 4(m – 1) = 4m + 5\)
\(Δ <0\Leftrightarrow m < – {5 \over 4}\) : Phương trình vô nghiệm
\(Δ = 0 \Leftrightarrow m = – {5 \over 4}\) : Phương trình có nghiệm kép là:
\({x_1} = {x_2} = – {b \over {2a}} = {{ – 3} \over {2(m – 1)}} = {{ – 3} \over {2( – {5 \over 4} – 1)}} = {2 \over 3}\)
\(Δ > 0 \Leftrightarrow m > – {5 \over 4}\) : Phương trình có hai nghiệm phân biệt là \(x _{1,2}= {{ – 3 \pm \sqrt {4m + 5} } \over {2(m – 1)}}\)
b) \({x^2} – {\rm{ }}4x{\rm{ }} + {\rm{ }}m{\rm{ }} – {\rm{ }}3{\rm{ }} = {\rm{ }}0\)
Ta có: \(Δ’ = 4 – (m – 3) = 7 – m\)
+ \(Δ’ < 0 ⇔ m > 7\) : Phương trình vô nghiệm
+ \(Δ’= 0 ⇔ m = 7\) : Phương trình có nghiệm kép: \({x_1} = {x_2} = – {b \over {2a}} = {4 \over 2} = 2\)
+ \(Δ’> 0 ⇔ m < 7\) : Phương trình có hai nghiệm phân biệt: \(x_{1,2} = 2 \pm \sqrt {7 – m} \)

