Bài 5: Cho O là tâm đường tròn ngoại tiếp tam giác đều MNP. Góc nào sau đây bằng \({120^0}\) ?
(A) \((\overrightarrow {MN} ,\,\overrightarrow {NP} )\);
(B) \((\overrightarrow {MO} ,\,\overrightarrow {ON} )\);
(C) \((\overrightarrow {MN} ,\,\overrightarrow {OP} )\);
(D) \((\overrightarrow {MN} ,\,\overrightarrow {MP} )\).

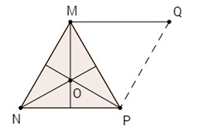
Vẽ \(\overrightarrow {MQ} = \overrightarrow {NP} \,\,;\,\,(\overrightarrow {MN} ,\,\overrightarrow {NP} ) = (\overrightarrow {MN} ,\,\overrightarrow {MQ} ) = {120^0}\).
Chọn (A).
Bài 6: Cho M, N, P, Q là bốn điểm tùy ý. Trong các hệ thức sau, hệ thức nào sai ?
Advertisements (Quảng cáo)
(A) \(\overrightarrow {MN} (\overrightarrow {NP} + \overrightarrow {PQ} ) = \overrightarrow {MN} .\overrightarrow {NP} + \overrightarrow {MN} .\overrightarrow {PQ} \);
(B) \(\overrightarrow {MP} .\overrightarrow {MN} = – \overrightarrow {MN} .\overrightarrow {MP} \);
(C) \(\overrightarrow {MN} .\overrightarrow {PQ} = \overrightarrow {PQ} .\overrightarrow {MN} \);
(D) \((\overrightarrow {MN} – \overrightarrow {PQ} ).(\overrightarrow {MN} + \overrightarrow {PQ} ) = M{N^2} – P{Q^2}\).

Advertisements (Quảng cáo)
Chọn (B).
Bài 7: Trong các hệ thức sau, hệ thức nào đúng ?
(A) \(|\overrightarrow a .\,\overrightarrow b | = |\overrightarrow a |.|\overrightarrow b |\);
(B) \(\sqrt {{{\overrightarrow a }^2}} = |\overrightarrow a |\);
(C) \(\sqrt {{{\overrightarrow a }^2}} = \overrightarrow a \) ;
(D) \(\overrightarrow a = \pm |\overrightarrow a |\).

Ta có \(\sqrt {{{\overrightarrow a }^2}} = \sqrt {|\overrightarrow a {|^2}} = |\overrightarrow a |\) .
Chọn (B)
Bài 8: Trong mặt phẳng tọa độ, cho \(\overrightarrow a = (3\,;\,4),\,\,\overrightarrow b = (4\,;\, – 3)\). Kết luận nào sau đây là sai ?
(A) \(\overrightarrow a .\,\overrightarrow b = 0\) (B) \(\overrightarrow a \bot \overrightarrow b \);
(C) \(|\overrightarrow a .\,\overrightarrow b | = 0\); (D) \(|\overrightarrow a |.|\overrightarrow b | = 0\).

Ta có \(|\overrightarrow a |.|\overrightarrow b | = \sqrt {{3^2} + {4^2}} .\sqrt {{4^2} + {{( – 3)}^2}} = 25\). Chọn (D).

