Bài 5: a) Lập bảng biến thiên và vẽ đồ thị (p) của : y = x2 + x – 6
b) Biện luận theo m số giao điểm của (P) và đường thẳng (d): y = 2x + m
c) Khi (d) và (P) cắt nhau, gọi A và B là giao điểm, hãy tìm tọa độ trung điểm của đoạn thẳng AB.
Đáp án
a) Bảng biến thiên:
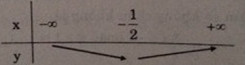
Đồ thị hàm số:
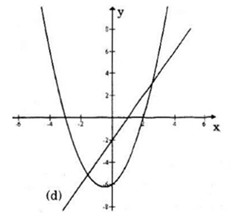
b) Số giao điểm của parabol (P) với đường thẳng (d) đúng bằng số nghiệm của phương trình:
x2 + x- 6 = 2x + m hay x2 – x – 6 – m = 0 (1)
Phương trình (1) có biệt thức:
Δ = 1 + 4(6 + m) = 4m + 25
Do đó:
+ Nếu \(m < – {{25} \over 4} \Rightarrow \Delta < 0\) thì phương trình (1) vô nghiệm
Do đó, (P) và (d) không có điểm chung
+ Nếu \(m = – {{25} \over 4} \Rightarrow \Delta =0\) thì phương trình (1) có 1 nghiệm kép duy nhất
Do đó, (P) và (d) có 1 điểm chung
+ Nếu \(m > – {{25} \over 4} \Rightarrow \Delta > 0\) thì phương trình (1) có hai nghiệm phân biệt
c) Giả sử (P) và (d) cắt nhau tại hai điểm phân biệt. Khi đó hoành độ của A và B chính là hai nghiệm của phương trình (1), gọi chúng là x1 và x2.
Hơn nữa, A và B là hai điểm của đường thẳng (d) nên tọa độ của chúng là:
Advertisements (Quảng cáo)
\(A({x_1};\,2{x_1} + m)\,;\,\,\,B({x_2};\,2{x_2} + m)\,\,\,(m > – {{25} \over 4})\)
Vậy trung điểm của đoạn thẳng AB có tọa độ là: \(I({{{x_1} + {x_2}} \over 2};\,{x_1} + {x_2} + m)\)
Theo định lý Vi-ét, ta có: x1 + x2 = 1
Tọa độ điểm I là \(({1 \over 2};\,1 + m)\,\,\,\,(m > – {{25} \over 4})\)
Bài 6: Cho phương trình : 2x2 + (k – 9)x + k2 + 3k + 4 =0 (1)
a) Tính k biết rằng (1) có 2 nghiệm trùng nhau
b) Tính nghiệm gần đúng của (1) với \(k = – \sqrt 7 \) (chính xác đến hàng phần nghìn)
Đáp án
a) Phương trình (1) có nghiệm trùng nhau
\( \Leftrightarrow \Delta = – 7({k^2} + 6k – 7) = 0 \Leftrightarrow \left[ \matrix{
k = 1 \hfill \cr
k = – 7 \hfill \cr} \right.\)
b) Khi \(k = – \sqrt 7 \) , \(\Delta =42\sqrt7\) phương trình đã cho có hai nghiệm là:
\(\left[ \matrix{
{x_1} = {{9 + \sqrt 7 – \sqrt {42\sqrt 7 } } \over 4} \approx 0,276 \hfill \cr
{x_2} = {{9 + \sqrt 7 + \sqrt {42\sqrt 7 } } \over 4} \approx 5,547 \hfill \cr} \right.\)
Bài 7: Cho phương trình: \({x^2} + 2(\sqrt 3 + 1)x + 2\sqrt 3 = 0\)
Advertisements (Quảng cáo)
a) Không giải phương trình, tính gần đúng tổng các bình phương hai nghiệm của phương trình (chính xác đến hàng phần trăm)
b) Tính nghiệm gần đúng của phương trình (chính xác đến hàng phần trăm).
Đáp án
a) Theo định lý Vi-ét, ta có:
\(\eqalign{
& \left\{ \matrix{
{x_1} + {x_2} = – 2(\sqrt 3 + 1) \hfill \cr
{x_1}{x_2} = 2\sqrt 3 \,\,\,(\Delta ‘ > 0) \hfill \cr} \right. \cr
& \Rightarrow x_1^2 + x_2^2 = {({x_1} + {x_2})^2} – 2{x_1}{x_2} \cr&= 4{(\sqrt 3 + 1)^2} – 4\sqrt 3 = 4(4 + \sqrt 3 ) \approx 22,93 \cr} \)
b) \(x_1≈ -0, 73;x_2≈ -4, 73\)
Bài 8: Biện luận theo tham số m số nghiệm và dấu các nghiệm của phương trình
a) x2 + 4(m + 3)x + 6(m2 – 5m + 6) = 0
b) (m – 1)x2 – (m – 3)x – m – 3 = 0
Đáp án
a) Ta có:
Δ’ = 4(m + 3)2 – 6(m2 – 5m + 6) = -2m2 + 54m
S = 4(m + 3); P = 6(m2 – 5m + 6)
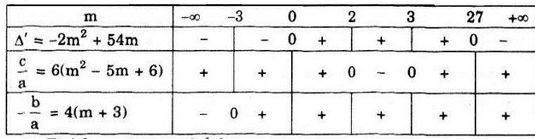
Bảng trên dẫn đến kết luận sau:
+ Nếu m < 0 hoặc m > 27 thì Δ’ < 0 nên phương trịnh vô nghiệm.
+ Nếu m = 0 hoặc m = 27 thì \(\Delta ‘ = 0;\,\,{c \over a} > 0;\,\, – {b \over a} > 0\) nên phương trình có một nghiệm dương (nghiệm kép)
+ Nếu 0 < m < 2 hoặc 3 < m < 27 thì \(\Delta ‘ > 0;\,\,{c \over a} > 0;\,\, – {b \over a} > 0\) nên phương trình có hai nghiệm dương phân biệt.
+ Nếu 2 < m < 3 thì \({c \over a} < 0\) nên phương trình có hai nghiệm trái dấu.
+ Nếu m = 2 hoặc m = 3 thì \({c \over a} = 0\,\,;{{ – b} \over a} > 0\) nên phương trình có một nghiệm bằng 0 và một nghiệm dương.
b) Khi m = 1, ta có phương trình 2x – 4 = 0. Phương trình có một nghiệm dương.
Khi m ≠ 1, ta có phương trình bậc hai. Số nghiệm và dấu của các nghiệm phụ thuộc vào dấu của các biểu thức sau:
\(\eqalign{
& \Delta = {(m – 3)^2} + 4(m – 1)(m + 3) \cr&= 5{m^2} + 2m – 3 \cr
& P = {c \over a} = {{ – m – 3} \over {m – 1}} \cr
& S = – {b \over a} = {{m – 3} \over {m – 1}} \cr} \)
Ta có bảng xét dấu:
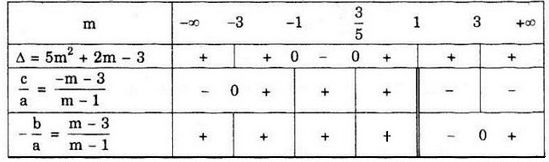
Từ bảng xét dấu, ta suy ra:
+ Nếu \( – 1 < m < {3 \over 5}\) thì Δ < 0 nên phương trình vô nghiệm
+ Nếu m < -3 hoặc m > 1 thì \({c \over a} < 0\) nên phương trình có hai nghiệm trái dấu.
+ Nếu -3 < m < -1 hoặc \({3 \over 5} < m < 1\) thì \(\Delta > 0;\,{c \over a} > 0;\,{{ – b} \over a} > 0\) nên phương trình có hai nghiệm dương phân biệt.
+ Nếu m = -3 thì \(\,{c \over a} = 0;\,{{ – b} \over a} > 0\) nên phương trình có một nghiệm x = 0, nghiệm kia là nghiệm dương
+ Nếu m = -1 hoặc \(m = {3 \over 5}\) thì \(\Delta = 0;\,{c \over a} > 0;\,{{ – b} \over a} > 0\) nên phương trình có một nghiệm kép dương.

