Chứng minh các đăng thức sau
a) \((\overrightarrow {A{A’}} + \overrightarrow {B{B’}} ).\,\overrightarrow {AC} = 0\)
b) \((\overrightarrow {A{A’}} + \overrightarrow {B{B’}} + \overrightarrow {C{C’}} ).\,\overrightarrow {AC} = 0\)
c) \(\overrightarrow {A{A’}} + \overrightarrow {B{B’}} + \overrightarrow {C{C’}} = 0\)
d) \(\overrightarrow {A{B_1}} + \overrightarrow {B{C_1}} + \overrightarrow {C{A_1}} = 0\)
Giải
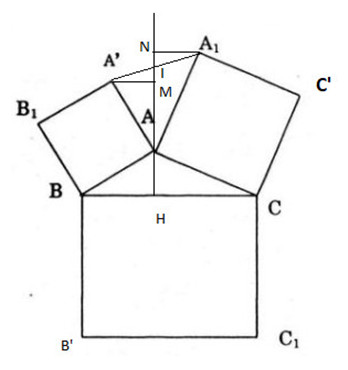
a) Kẻ \(AH \bot BC\) ta chứng minh đường thẳng AH cắt A’A1 tại trung điểm I của A’A1. Kẻ .
Ta có: \({A’}M \bot AH\,,\,\,{A_1}N \bot AH\)
\(\eqalign{
& \Delta AHB = \Delta {A’}MA\,\,\, \Rightarrow \,\,{A’}M = AH \cr
& \Delta AHC = \Delta {A_1}NA\,\,\, \Rightarrow \,\,{A_1}N = AH \cr} \)
Từ đó suy ra: \(\Delta IM{A’} = \Delta IN{A_1}\,\,\, \Rightarrow \,\,I{A’} = \,\,I{A_1}\,\)
Tương tự gọi J là trung điểm \({B_1}{B’}\) thì \(BJ \bot AC\) .
Ta có
\(\overrightarrow {A{A’}} + \overrightarrow {B{B’}} = \overrightarrow {B{B_1}} + \overrightarrow {B{B’}} = 2\overrightarrow {BJ} \)
Advertisements (Quảng cáo)
\(\Rightarrow \,\,(\overrightarrow {A{A’}} + \overrightarrow {B{B’}} ).\,\overrightarrow {AC} = 0\)
b) Theo câu a) và \(\overrightarrow {C{C’}} \bot \overrightarrow {AC} \) nên \((\overrightarrow {A{A’}} + \overrightarrow {B{B’}} + \overrightarrow {C{C’}} ).\,\overrightarrow {AC} = 0\) .
c) Đặt \(\overrightarrow u = \overrightarrow {A{A’}} + \overrightarrow {B{B’}} + \overrightarrow {C{C’}} \).
Ta có \(\overrightarrow u .\,\overrightarrow {AC} = 0\,,\,\overrightarrow u .\,\overrightarrow {AB} = 0\,\) . Suy ra \(\overrightarrow u = \overrightarrow 0 \) .
d) Ta có
\(\eqalign{
& \overrightarrow {A{B_1}} + \overrightarrow {B{C_1}} + \overrightarrow {C{A_1}}\cr& = \overrightarrow {A{A’}} + \overrightarrow {AB} + \overrightarrow {B{B’}} + \overrightarrow {BC} + \overrightarrow {C{C’}} + \overrightarrow {CA} \cr
& = \overrightarrow {A{A’}} + \overrightarrow {B{B’}} + \overrightarrow {C{C’}} + \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow 0 \cr} \)
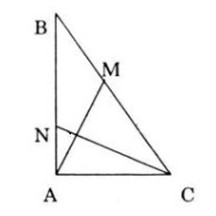
Bài 2: Cho tam giác vuông tại A, AB = c, AC = b . Gọi M là điểm trên cạnh BC sao cho CM = 2BM, N là điểm trên cạnh AB sao cho BN = 2AN (h.106).
a) Biểu thị các vectơ theo hai vectơ \(\overrightarrow {AM} ,\,\overrightarrow {CN} \) và \(\overrightarrow {AB} ;\,\overrightarrow {AC} \) .
Advertisements (Quảng cáo)
b) Tìm hệ thức liên hệ giữa b và c sao cho \(AM \bot CN\) .
Giải
a) Ta có:
\(\overrightarrow {CM} = 2\overrightarrow {MB} \,\,\, \Rightarrow \,\,\overrightarrow {AM} – \overrightarrow {AC} = 2(\overrightarrow {AB} – \overrightarrow {AM} )\)
\(\Rightarrow \,\,\overrightarrow {AM} = {2 \over 3}\overrightarrow {AB} + {1 \over 3}\overrightarrow {AC} \)
Mặt khác \(\overrightarrow {BN} = 2\overrightarrow {NA} \,\, \Rightarrow \,\,\overrightarrow {AN} – \overrightarrow {AB} = – 2\overrightarrow {AN} \)
\(\Rightarrow \,\,\overrightarrow {AN} = {1 \over 3}\overrightarrow {AB} \)
\( \Rightarrow \,\,\overrightarrow {CN} = \overrightarrow {AN} – \overrightarrow {AC} = {1 \over 3}\overrightarrow {AB} – \overrightarrow {AC} \)
b) Ta có
\(\eqalign{
& \overrightarrow {AM} \bot \overrightarrow {CN} \Leftrightarrow \,\,\overrightarrow {AM} .\overrightarrow {CN} = 0\cr& \Leftrightarrow \,\,\left( {{2 \over 3}\overrightarrow {AB} + {1 \over 3}\overrightarrow {AC} } \right)\left( {{1 \over 3}\overrightarrow {AB} – \overrightarrow {AC} } \right) \cr&\;\;\;\;\;= 0 \cr
& \Leftrightarrow \,\,{2 \over 9}A{B^2} – {2 \over 3}\overrightarrow {AB} .\overrightarrow {AC} + {1 \over 9}\overrightarrow {AC} .\,\overrightarrow {AB} – {1 \over 3}A{C^2}\cr&\;\;\;\;\; = 0 \cr
& \Leftrightarrow \,\,{2 \over 9}{c^2} – {1 \over 3}{b^2} = 0 \cr
& \ \Leftrightarrow \,\,2{c^2} = 3{b^2} \cr} \)
Bài 3: Cho tam giác ABC với AB = 4; AC = 5, BC = 6 .
a) Tính các góc A, B, C.
b) Tính độ dài các đường trung tuyến và diện tích tam giác.
c) Tính các bán kính đường tròn nội tiếp và ngoại tiếp tam giác .
Giải
a) Ta có \(a = 6, b = 5, c = 4\)
\(\eqalign{
& \cos A = {{{b^2} + {c^2} – {a^2}} \over {2bc}} = {{{5^2} + {4^2} – {6^2}} \over {2.5.4}} = {1 \over 8}\cr& \Rightarrow \widehat A \approx {83^0} \cr
& \cos B = {{{a^2} + {c^2} – {b^2}} \over {2ac}} = {{{6^2} + {4^2} – {5^2}} \over {2.6.4}} = {9 \over {16}}\cr& \Rightarrow \widehat B \approx {56^0} \cr
& \Rightarrow \,\,\widehat C \approx {41^0} \cr} \)
b) Ta có
\(\eqalign{
& m_a^2 = {1 \over 4}\left( {2{b^2} + 2{c^2} – {a^2}} \right) \cr&\;\;\;\;\;\;= {1 \over 4}\left( {50 + 32 – 36} \right) = {{46} \over 4}\,\, \Rightarrow \,\,{m_a} = {{\sqrt {46} } \over 2} \cr
& m_b^2 = {1 \over 4}\left( {2{a^2} + 2{c^2} – {b^2}} \right) = {{79} \over 4}\,\, \Rightarrow \,\,{m_b} = {{\sqrt {79} } \over 2} \cr
& \Rightarrow \,\,{m_c} = {{\sqrt {106} } \over 2} \cr} \)

