Bài 9: Giải và biện luận các phương trình
a) \({{mx – m – 3} \over {x + 1}} = 1\)
b) \(|(m + 1)x – 3 | = |x + 2|\)
c) \((mx + 1)\sqrt {x – 1} = 0\)
Đáp án
a) Điều kiên: \(x ≠ 1\)
Ta có:
\({{mx – m – 3} \over {x + 1}} = 1 \Leftrightarrow mx – m – 3 = x + 1\)
\(\Leftrightarrow (m – 1)x = m + 4\)
+ Nếu m ≠ 1 thì \(x = {{m + 4} \over {m – 1}}\) . Nghiệm \(x = {{m + 4} \over {m – 1}}\) nhận được:
\( \Leftrightarrow {{m + 4} \over {m – 1}} \ne – 1 \Leftrightarrow m + 4 \ne 1-m \Leftrightarrow m \ne – {3 \over 2}\)
+ Nếu m = 1: phương trình vô nghiệm
Vậy:
Với m ≠ 1 và \(m \ne – {3 \over 2}:\,\,\,S = {\rm{\{ }}{{m + 4} \over {m – 1}}{\rm{\} }}\)
Với m = 1 hoặc \(m = – {3 \over 2}:\,\,\,\,S = \emptyset \)
b) Ta có:
\(|(m + 1)x – 3 | = |x + 2| \)
\( \Leftrightarrow \left[ \matrix{
(m + 1)x – 3 = x + 2 \hfill \cr
(m + 1)x – 3 = – x – 2 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
mx = 5 \hfill \cr
(m + 2)x = 1 \hfill \cr} \right.\)
Vậy \(m = 0;\,\,S = {\rm{\{ }}{1 \over 2}{\rm{\} }}\)
+ Với m = -2; \(S = {\rm{\{ – }}{5 \over 2}{\rm{\} }}\)
+ Với m ≠ 0 và m ≠ -2 thì \(S = {\rm{\{ }}{5 \over m};\,\,{1 \over {m + 2}}{\rm{\} }}\)
c) Điều kiện: x ≥ 1
\((mx + 1)\sqrt {x – 1} = 0 \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
mx + 1 = 0\,\,\,\,\,\,\,\,\,\,\,\,(1) \hfill \cr} \right.\,\,\,\,\)
+ Với m = 0 thì phương trình (1) vô nghiệm. Do đó: S = {1}
+ Với m ≠ 0 thì (1) có nghiệm là \(x = – {1 \over m}\) , nghiệm này nhận được:
\( \Leftrightarrow – {1 \over m} \ge 1 \Leftrightarrow {{m + 1} \over m} \le 0 \Leftrightarrow – 1 \le m < 0\)
Vậy: với m < -1 hoặc m ≥ 0 thì S = {1}
-1 ≤ m < 0 thì \(S = {\rm{\{ }}1, – {1 \over m}{\rm{\} }}\)
Bài 10: a) Lập phương trình bậc hai có hai nghiệm x1 và x2 thỏa mãn các hệ thức :
x1 + x2 + x1x2=0;
Advertisements (Quảng cáo)
m(x1 + x2 ) – x1x2 = 3m + 4
b) Xét dấu các nghiệm phương trình đó tùy theo m.
Đáp án
a) Đặt S = x1 + x2 và P = x1x2
Các điều kiện của bài toán được thể hiện qua hệ phương trình (ẩn S và P)
\(\left\{ \matrix{
S + P = 0 \hfill \cr
mS – P = 3m + 4 \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{
S + P = 0 \hfill \cr
S(m + 1) = 3m + 4\,\,\,(1) \hfill \cr} \right.\)
+ Khi m = -1 thì (1) vô nghiệm, nghĩa là không có nghiệm nào thỏa mãn điều kiện của bài toán.
+ Khi m ≠ -1, hệ (1) có một nghiệm \((S, P) = ({{3m + 4} \over {m + 1}};\,{{ – 3m + 4} \over {m + 1}})\,\,\,\,(2)\)
Vậy phương trình cần tìm là:
\(\eqalign{
& {x^2} – Sx + P = 0 \cr
& \Leftrightarrow {x^2} – {{3m + 4} \over {m + 1}}x – {{3m + 4} \over {m + 1}} = 0 \cr
& \Leftrightarrow (m + 1){x^2} – (3m + 4)x – (3m + 4) = 0\,\,\,\,\,\,\,(3) \cr} \)
Điều kiện để phương trình (3) có nghiệm là:
\(\eqalign{
& \Delta = {(3m + 4)^2} + 4(m + 1)(3m + 4) \cr&= (3m + 4)(7m + 8) \ge 0 \cr
& \Leftrightarrow \left[ \matrix{
m \le – {4 \over 3} \hfill \cr
m \ge – {8 \over 7} \hfill \cr} \right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(4) \cr} \)
Tóm lại, phương trình cần tìm là phương trình (3) với điều kiện của m là m ≠ -1 và thỏa mãn (4).
b) Ta có:
\(S = – P = {{3m + 4} \over {m + 1}} \Leftrightarrow \left[ \matrix{
m < – {4 \over 3} \hfill \cr
m > – 1 \hfill \cr} \right.\)
Kết hợp với điều kiện (4) , ta suy ra:
+ Nếu
\(\left[ \matrix{
m < – {4 \over 3} \hfill \cr
m > – 1 \hfill \cr} \right.\)
thì P < 0 nên (3) có hai nghiệm trái dấu
Advertisements (Quảng cáo)
+ Nếu \(m = – {4 \over 3}\) thì phương trình (3) có một nghiệm kép x = 0
+ Nếu \( – {8 \over 7} \le m < 1\) thì P > 0; S < 0 nên phương trình (3) có hai nghiệm âm.
+Nếu \( – {4 \over 3} < m < – {8 \over 7}\) thì phương trình (3) vô nghiệm.
Bài 11: Giải và biện luận các hệ phương trình
a)
\(\left\{ \matrix{
(m + 3)x + 2y = m \hfill \cr
(3m + 1)x + (m + 1)y = 1 \hfill \cr} \right.\)
b)
\(\left\{ \matrix{
(2m + 3)x + 5y = m – 11 \hfill \cr
(m + 2)x + 2y = m – 2 \hfill \cr} \right.\)
Đáp án
a) Ta có:
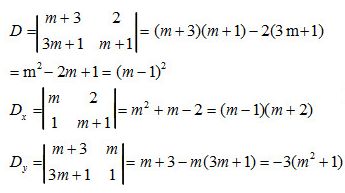
+ Nếu m ≠ 1 thì hệ có nghiệm (x, y) với:
\(\eqalign{
& x = {{{D_x}} \over D} = {{(m – 1)(m + 2)} \over {{{(m – 1)}^2}}} = {{m + 2} \over {m – 1}} \cr
& y = {{{D_y}} \over D} = {{ – 3({m^2} – 1)} \over {{{(m – 1)}^2}}} = {{ – 3(m + 1)} \over {m – 1}} \cr} \)
+ Nếu m = 1 thì hệ thành
\(\left\{ \matrix{
4x + 2y = 1 \hfill \cr
4x + 2y = 1 \hfill \cr} \right. \Leftrightarrow y = – 2x + {1 \over 2}\)
Hệ có vô số nghiệm \((x,\, – 2x + {1 \over 2})\) với x ∈ R
b) Ta có:
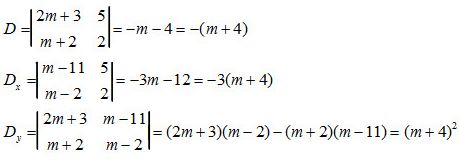
+Với \(m ≠ -4\) thì hệ có nghiệm (x, y) với:
\(\eqalign{
& x = {{{D_x}} \over D} = {{ – 3(m + 4)} \over { – (m + 4)}} = 3 \cr
& y = {{{D_y}} \over D} = {{{{(m + 4)}^2}} \over { – (m + 4)}} = – m – 4 \cr} \)
+ Với \(m = -4\), hệ có vô số nghiệm với \((x; x – 3), x ∈ \mathbb R\)
Bài 12: Giải các hệ phương trình
a)
\(\left\{ \matrix{
{x^2} – 5xy + {y^2} = 7 \hfill \cr
2x + y = 1 \hfill \cr} \right.\)
b)
\(\left\{ \matrix{
{x^2} + {y^2} + x + y = 8 \hfill \cr
x + y + xy = 5 \hfill \cr} \right.\)
c)
\(\left\{ \matrix{
{x^2} + {y^2} – x + y = 2 \hfill \cr
xy + x – y = – 1 \hfill \cr} \right.\)
Đáp án
a) Từ phương trình thứ hai của hệ, ta được \(y = 1- 2x\)
Thay vào phương trình thứ nhất ta được:
\(\eqalign{
& {x^2} – 5x(1 – 2x) + {(1 – 2x)^2} = 7 \cr
& \Leftrightarrow 15{x^2} – 9x – 6 = 0 \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
x = – {2 \over 5} \hfill \cr} \right. \cr} \)
+ Với \(x = 1\) thì \(y = 1 – 2.1 = -1\)
+ Với \(x = – {2 \over 5} \Rightarrow y = 1 – 2.( – {2 \over 5}) = {9 \over 5}\)
Vậy hệ có hai nghiệm: \((-1, 1)\) và \(( – {2 \over 5};\,{9 \over 5})\)
b) Đặt \(S = x + y; P = xy\). Ta có:
\(\left\{ \matrix{
{S^2} – 2P + S = 8 \hfill \cr
S + P = 5 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
P = 5 – S \hfill \cr
{S^2} + 3S – 18 = 0 \hfill \cr} \right.\)
\(\Leftrightarrow \left[ \matrix{
\left\{ \matrix{
S = 3 \hfill \cr
P = 2 \hfill \cr} \right. \hfill \cr
\left\{ \matrix{
S = – 6 \hfill \cr
P = 11 \hfill \cr} \right. \hfill \cr} \right.\)
+ Với S = 3, P = 2, hệ có nghiệm (2, 1) và (1, 2)
+ Với S = -6, P = 11 vô nghiệm do S2 – 4P < 0
c) Đặt \(S = x – y; P = xy\). Ta có:
\(\left\{ \matrix{
{S^2} + 2P – S = 2 \hfill \cr
P + S = – 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
P = 1 – S \hfill \cr
{S^2} – 3S – 4 = 0 \hfill \cr} \right. \)
\(\Leftrightarrow \left[ \matrix{
\left\{ \matrix{
S = – 1 \hfill \cr
P = 0 \hfill \cr} \right. \hfill \cr
\left\{ \matrix{
S = 4 \hfill \cr
P = – 5 \hfill \cr} \right. \hfill \cr} \right.\)
+ Với \(S = -1, P = 0\) thì \(x, -y\) là nghiệm phương trình:
\({X^2} + X = 0 \Leftrightarrow \left[ \matrix{
X = 0 \hfill \cr
X = – 1 \hfill \cr} \right.\)
Ta có nghiệm (0, 1) và (-1, 0)
+ Với \(S = 4, P = -5: x; -y\) là nghiệm phương trình:
X2 – 4X + 5 = 0 (vô nghiệm)

