Bài 4: Trong các trường hợp nào tích vô hướng \(\overrightarrow a .\overrightarrow b \) có giá trị dương, có giá trị âm, bằng \(0\) ?

Ta có \(\overrightarrow a .\,\overrightarrow b = \left| {\overrightarrow a } \right|.\,\left| {\overrightarrow b } \right|.\cos (\overrightarrow a ,\,\overrightarrow b )\), do đó
+) \(\overrightarrow a .\,\overrightarrow b > 0\) khi \(\overrightarrow a ,\,\overrightarrow b \) khác \(\overrightarrow 0 \) và góc \((\overrightarrow a ,\,\overrightarrow b ) < {90^0}\);
+) \(\overrightarrow a .\,\overrightarrow b < 0\) khi \(\overrightarrow a ,\,\overrightarrow b \) khác \(\overrightarrow 0 \) và góc \((\overrightarrow a ,\,\overrightarrow b ) > {90^0}\);
+) \(\overrightarrow a .\,\overrightarrow b = 0\,\, \Leftrightarrow \,\,\overrightarrow a \bot \overrightarrow {b.}\)
Bài 5: Cho tam giác \(ABC\). Tổng \((\overrightarrow {AB} ,\,\overrightarrow {BC} ) + (\overrightarrow {BC} ,\,\overrightarrow {CA} ) + (\overrightarrow {CA} ,\,\overrightarrow {AB} )\) có thể nhận giá trị nào trong các giá trị sau : \({90^0}\,;\,{180^0}\,;\,{270^{0\,}}\,;\,{360^0}\) ?

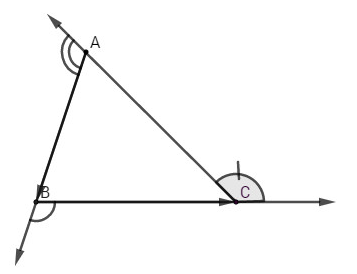
Ta có
\((\overrightarrow {AB} ,\,\overrightarrow {BC} ) = {180^0} – \widehat B\,\,;\,\,(\overrightarrow {BC} ,\,\overrightarrow {CA} ) = {180^0} – \widehat C\,\,;\,\,(\overrightarrow {CA} ,\,\overrightarrow {AB} ) = {180^0} – \widehat A\)
Advertisements (Quảng cáo)
Do đó \((\overrightarrow {AB} ,\,\overrightarrow {BC} ) + (\overrightarrow {BC} ,\,\overrightarrow {CA} ) + (\overrightarrow {CA} ,\,\overrightarrow {AB} ) = {360^0}\)
Bài 6: Cho tam giác \(ABC\) vuông ở \(A\) và \(\widehat B = {30^0}\). Tính giá trị của các biểu thức sau
a) \(\cos (\overrightarrow {AB} ,\,\overrightarrow {BC} ) + \sin (\overrightarrow {BA} ,\,\overrightarrow {BC} ) + \tan {{(\overrightarrow {AC} ,\,\overrightarrow {CB} )} \over 2}\);
b) \(\sin (\overrightarrow {AB} ,\,\overrightarrow {AC} ) + \cos (\overrightarrow {BC} ,\,\overrightarrow {BA} ) + \cos (\overrightarrow {CA} ,\,\overrightarrow {BA} )\).

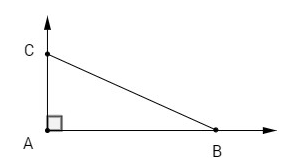
Advertisements (Quảng cáo)
a) Ta có
\((\overrightarrow {AB} ,\,\overrightarrow {BC} ) = {150^0}\,\,;\,\,\,(\overrightarrow {BA} ,\,\overrightarrow {BC} ) = {30^0}\,\,;\,\,\,(\overrightarrow {AC} ,\,\overrightarrow {CB} ) = {120^0}\)
Do đó
\(\eqalign{
& \cos (\overrightarrow {AB} ,\,\overrightarrow {BC} ) + \sin (\overrightarrow {BA} ,\,\overrightarrow {BC} ) + \tan {{(\overrightarrow {AC} ,\,\overrightarrow {CB} )} \over 2} = \cos {150^0} + {\mathop{\rm s}\nolimits} {\rm{in3}}{{\rm{0}}^0} + \tan {60^0} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,{{ – \sqrt 3 } \over 2} + {1 \over 2} + \sqrt 3 = {{\sqrt 3 + 1} \over 2} \cr} \)
b) Ta có \((\overrightarrow {CA} ,\,\overrightarrow {BA} ) = {90^0}\) ,do đó
\(\eqalign{
& \sin (\overrightarrow {AB} ,\,\overrightarrow {AC} ) + \cos (\overrightarrow {BC} ,\,\overrightarrow {BA} ) + \cos (\overrightarrow {CA} ,\,\overrightarrow {BA} ) = \sin {90^0} + \cos {30^0} + \cos {90^0} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 1 + {{\sqrt 3 } \over 2} + 0 = {{2 + \sqrt 3 } \over 2} \cr} \)
Bài 7: Cho bốn điểm bất kì \(A, B, C, D\). Chứng minh rằng
\(\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} = 0\).
Từ đó suy ra một cách chứng minh định lí: “Ba đường cao của một tam giác đồng quy”.

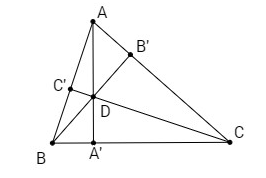
Ta có
\(\eqalign{
& \,\,\,\,\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} \cr
& = \overrightarrow {DA} (\overrightarrow {DC} – \overrightarrow {DB} ) + \overrightarrow {DB} (\overrightarrow {DA} – \overrightarrow {DC} ) + \overrightarrow {DC} (\overrightarrow {DB} – \overrightarrow {DA} ) \cr
& = \overrightarrow {DA} \overrightarrow {DC} – \overrightarrow {DA} \overrightarrow {DB} + \overrightarrow {DB} \overrightarrow {DA} – \overrightarrow {DB} \overrightarrow {DC} + \overrightarrow {DC} \overrightarrow {DB} – \overrightarrow {DC} \overrightarrow {DA} = 0 \cr} \)
Gọi \(D\) là giao điểm của hai đường cao \(AA’, BB’\) của tam giác \(ABC\).
Ta có \(\overrightarrow {DA} .\overrightarrow {BC} = 0\,;\,\,\overrightarrow {DB} .\overrightarrow {CA} = 0\)
Từ đó suy ra \(\overrightarrow {DC} .\overrightarrow {AB} = 0\), do đó \(DC \bot AB\). Vậy \(D\) nằm trên đường cao \(CC’\) của tam giác \(ABC\), tức là ba đường cao trong tam giác đồng quy.

