Câu C1
Người nhảy dù có rơi tự do không ?
Giải :
Người nhảy dù không rơi tự do khi đang ở tư thế như trong ảnh vì lực cản không khí là đáng kể.
Câu C2
Rơi tự do là chuyển động đều hay là nhanh dần ? Làm thế nào biết được điều đó ?
Rơi tự do là chuyển động nhanh dần
Muốn biết điều này , ta đo quãng đường đi được trong những khoảng thời gian bằng nhau liên tiếp . Sẽ thấy quãng đường đo tăng dần nhưng chứng tỏ vận tốc tăng ⇔ Chuyển động nhanh dần.
Câu C3
Hãy xác định yếu tố của vectơ gia tốc rơi tự do
Giải :
Các yếu tốc của vectơ gia tốc rơi tự do \(\overrightarrow g \):
– Điểm đặt tại vật ;
– Phương thẳng đứng , chiều hướng xuống ;
– Độ dài tỉ lệ với độ lớn của g ( theo kết quả thí nghiệm trong bảng 1 thì \(g \approx 9,75\,m/{s^2}\))
Advertisements (Quảng cáo)
Bài 1
Chọn câu sai
A. Khi vật rơi tự do mọi vật chuyển động hoàn toàn như nhau
B. Vật rơi tự do khi không chịu sức cản của không khí
C. Người nhảy dù trên hình 6 .2 đang rơi tự do
D. Mọi vật chuyển động gần mặt dất đều chịu gia tốc rơi tự do
Giải :
Chọn C. Người nhảy dù trên hình 6 .2 đang rơi tự do
Bài 2
Một vật rơi tự do không vận tốc đầu từ độ cao 5 m . Tìm vận tốc của nó khi chạm đất
Advertisements (Quảng cáo)
Giải :
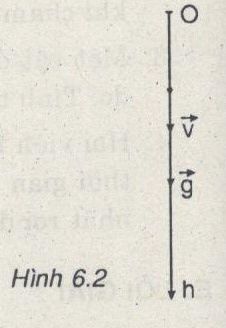
Chọn hệ tọa độ như hình vẽ : gốc O \( \equiv \) điểm thả vật
Gốc thời gian là lúc thả vật . Lấy g = 9,8 m/s2 (h.6.2)
Áp dụng công thức liên hệ , ta được :
\(v = \sqrt {2gh} = \sqrt {2.9,8.5} = 9,9(m/s)\)
Bài 3
Một vật được thả từ trên máy bay ở độ cao 80m . Cho rằng vật rơi tự do. Tính thời gian rơi.
Giải :
Rơi tự do từ độ cao h = 80 m so với đất.
Thời gian rơi : \(t = \sqrt {{{2h} \over g}} = \sqrt {{{2.80} \over {9,8}}} \approx 4,04(s)\)
Bài 4
Hai viên bi sắt được thả rơi từ cùng một độ cao cách nhau một khoảng thời gian 0,5s . Tính khoảng thời gian cách nhau giữa hai viên bi sau khi viên bi thứ nhất được rơi được 1 s ; 1,5 s
Giải :
Chọn hệ tọa độ gốc O trùng với điểm thả vật, gốc thời gian là lúc vật I bắt đầu rơi
Phương trình chuyển động của vật I :
\({h_1} = {{g{t^2}} \over 2} = 4,9{t^2}(s;m)\)
Phương trình chuyển động của vật II:
\({h_2} = {{g{{(t – 0,5)}^2}} \over 2} = 4,9{(t – 0,5)^2}(s;m)\)
Khoảng cách hai vật:
\(\left| {\Delta h} \right| = {h_1} – {h_2} = 4,9{t^2} – 4,9{(t – 0,5)^2} \)
\(= 4,9t – 1,225(s;m)\)
Tại t = 1s thì \(\left| {\Delta h} \right| = 4,9.1 – 1,225 = 3,675(m)\)
Tại t = 1,5s thì \(\left| {\Delta h} \right| = 4,9.1,5 – 1,225 = 6,125(m)\)

