Bài 1: Hãy tìm phát biểu sai
A. Quỹ đạo của một vật là tương đối , đối với các hệ quy chiếu khác nhau thì quỹ đạo của vật là khác nhau.
B. Vận tốc của vật là tương đối . Trong các hệ quy chiếu khác nhau thì vận tốc của cùng một vật là khác nhau.
C. Khoảng cách giữa hai điểm trong không gian là tương đối.
D. Tọa độ của một chất điểm phụ thuộc vào hệ quy chiếu.
Giải :
Chọn C
Bài 2: Một chiếc thuyền chuyển động ngược dòng với vận tốc 14 km/h so với mặt nước . Nước chảy với tốc độ 9km/h so với bờ. Hỏi vận tốc của thuyền so với bờ ? Một em bé đi từ đầu thuyền đến cuối thuyền với vận tốc 6 km/h so với thuyền. Hỏi vận tốc của em bé so với bờ ?
Giải
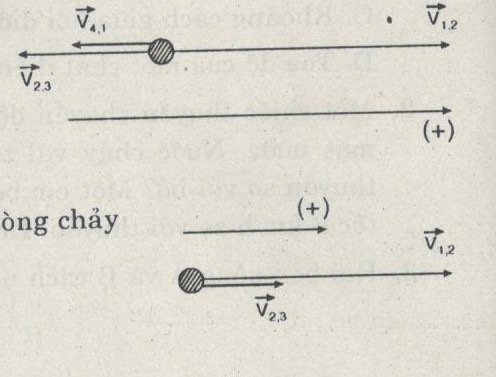
Coi thuyền là vật 1
Nước là vật 2
Bờ là vật 3
Em bé là vật 4
Thì có \({v_{13}} = {v_{12}} + {v_{23}}\) (1)
\({v_{14}} = {v_{12}} + {v_{23}} + {v_{34}} \Leftrightarrow – {v_{41}} = {v_{12}} + {v_{23}} – {v_{43}}\)
\( < = > {v_{43}} = {v_{12}} + {v_{23}} + {v_{41}}\) (2)
Advertisements (Quảng cáo)
Chọn chiều dương ngược chiều dòng nước thì
\({v_{12}} = 14km/h;{v_{23}} = – 9km/h;{v_{41}} = – 6km/h\)
Vận tốc của thuyền so với bờ :
\({v_{13}} = 14 – 9 = 5(km/h)\)
Vận tốc của em bé so với bờ :
\({v_{43}} = 14 – 9 – 6 = – 1(km/h)\)
\({v_{43}} < 0 < = > \overrightarrow {{v_{43}}} \) hướng theo chiều dòng chảy
Bài 3: Hai bến sông A và B cách nhau 18 km theo đường thẳng . Một chiếc ca nô phải mất bao nhiêu thời gian để đi từ A đến B rồi trở lại ngay từ B về A ? Biết rằng vận tốc của ca nô khi nước không chảy là 16 ,2 km/h và vận tốc của dòng nước so với bờ sông là 1,5 m/s
Giải :
Coi Ca nô là vật 1
Nước là vật 2
Advertisements (Quảng cáo)
Bờ là vật 3
Chọn chiều dương như hình vẽ
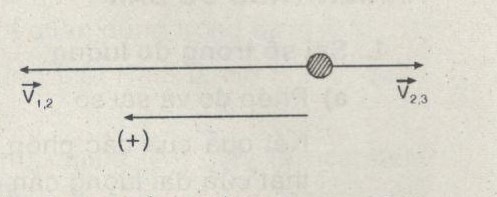
* Khi xuôi dòng :
Với \({v_{12}} = 16,2km/h;{v_{23}} = 5,4km/h\)
* Khi ngược dòng :
Với \({v_{12}} = 16,2km/h;{v_{23}} = – 5,4km/h\)
Áp dụng công thức vận tốc trong chuyển động thẳng đều và công thức cộng vận tốc :
Khi xuôi: \({{AB} \over {{t_1}}} = {v_{13}} = {v_{12}} + {v_{23}} \)
\(= > {t_1} = {{AB} \over {{v_{12}} + {v_{23}}}} = {{18} \over {16,2 + 5,4}} = {5 \over 6}(h)\)
Khi ngược :
\(\eqalign{ & {{AB} \over {{t_2}}} = {v_{13}} = {v_{12}} + {v_{23}}\cr&= > {t_2} = {{18} \over {16,2 – 5,4}} = {{5} \over 3}(h) \cr & t = {t_1} + {t_2} = 2,5h \cr} \)
Chú ý :
– Các đại lượng trong công thức \({v_{13}} = {v_{12}} + {v_{23}}\) là các đại lượng đại số.
– Nếu chọn chiều dương là chiều chuyển động của thuyền so với bờ để có độ dời ∆x = quãng đường S.
-Nếu biểu diễn các vectơ đã biết phương chiều \(\left( {\overrightarrow {{v_{23}}} ;\overrightarrow {{v_{12}}} } \right)\) vectơ nào cùng chiều dương sẽ có giá trị đại số dương và ngược lại.
Bài 4: Một người lái xuồng máy dự định mở máy cho xuôồng chạy ngang con sông rộng 240 m , mũi xuồng luôn luôn vuông góc với bờ sông . Nhưng do nước chảy nên xuồng sang đến bờ bên kia tại một địa điểm cách bến dự định 180 m về phía hạ lưu và xuồng đi hết 1 min. Xác định vận tốc của xuồng so với bờ sông.
Giải :
Coi xuồng là vật 1 ; Nước -2 ; Bờ -3
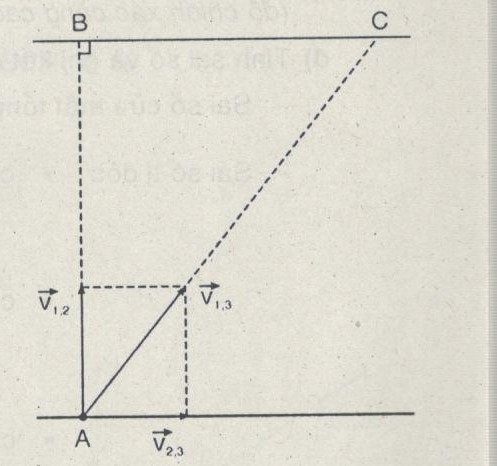
Có 2 cách giải sau
– Cách 1 : \(AC = \sqrt {A{B^2} + B{C^2}} = 300m\)
Vận tốc của xuồng so với bờ :
\({v_{13}} = {{AC} \over t} = {{300} \over {60}} = 5m/s\)
– Cách 2 :
\(\eqalign{ & {v_{23}} = {{BC} \over t} = {{180} \over {60}} = 3m/s \cr & {v_{12}} = {{AB} \over t} = {{240} \over {60}} = 4m/s \cr & {v_{13}} = \sqrt {v_{12}^2 + v_{23}^2} = 5m/s \cr} \)

