Câu 116: Tìm x, biết:
a) y + 30%y = -1, 3 b) \(y – 25\% y = {1 \over 2}\)
c) \(3{1 \over 3}y + 16{3 \over 4} = – 13,25\)
a) y + 30%y = -1, 3
(1+30%) y = -1, 3
\(\eqalign{
& {{130} \over {100}}y = – 1,3 \cr
& y = {{ – 13} \over {10}}:{{130} \over {100}} \cr
& y = {{ – 13} \over {10}}.{{100} \over {130}} = – 1 \cr} \)
b) \(y – 25\% y = {1 \over 2}\)
\(\left( {1 – 25\% } \right)y = {1 \over 2}\)
\(\eqalign{
& {{75} \over {100}}y = {1 \over 2} \cr
& y = {1 \over 2}:{{75} \over {100}} \cr
& y = {1 \over 2}.{{100} \over {75}} = {2 \over 3} \cr} \)
c) \(3{1 \over 3}y + 16{3 \over 4} = – 13,25\)
\(\eqalign{
& {{10} \over 3}y = – 13{1 \over 4} – 16{3 \over 4} \cr
& {{10} \over 3}y = – 30 \cr
& y = – 30:{{10} \over 3} = – 30.{3 \over {10}} = – 9 \cr} \)
Câu 117: Biết rằng tổng của mỗi hàng đều bằng 8,3 hãy điền số thích hợp vào các ô thay cho các chữ số a, b, c, d, e, g:
Advertisements (Quảng cáo)
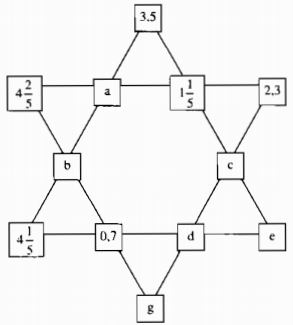
Ta có
\(4{2 \over 5} + a + 1{1 \over 5} + 2,3 = 8,3\)
\(\eqalign{
& \left( {4{2 \over 5} + 1{1 \over 5}} \right) + a = 6 \cr
& 5{3 \over 5} + a = 6 \Rightarrow a = 6 – 5{3 \over 5} = 5{5 \over 5} – 5{3 \over 5} = {2 \over 5} \cr
& 3,5 + a + b + 4{1 \over 5} = 8,3 \cr
& 3,5 + \left( {{2 \over 5} + 4{1 \over 5}} \right) + b = 8,3 \cr
& 4{3 \over 5} + b = 8,3 – 3,5 \cr
& 4,6 + b = 4,8 \Rightarrow b = 0,2 \cr
& 4{2 \over 5} + b + 0,7 + g = 8,3 \cr
& \left( {4,4 + 0,2 + 0,7} \right) + g = 8,3 \cr
& 5,3 + g = 8,3 \Rightarrow g = 8,3 – 5,3 = 3 \cr} \)
\(3,5 + 1,2 + c + e = 8,3 \)
\(\Rightarrow c + e = 8,3 – 4,7 = 3,6\) (1)
\(4,2 + 0,7 + d + e = 8,3 \)
Advertisements (Quảng cáo)
\(\Rightarrow d + e = 8,3 – 4,9 = 3,4\) (2)
\(2,3 + 3 + d + c = 8,3 \)
\(\Rightarrow c + d = 8,3 – 5,3 = 3\) (3)
Cộng từng vế (1), (2) và (3):
2 (c + d + e) = 3, 6 + 3, 4 + 3
c + d + e = 5
Suy ra: d = 1, 4; c = 1, 6; e = 2
Câu 118: Viết các phân số dưới \({7 \over {10}};{{10} \over {21}};{7 \over 8}\) dạng tổng các phân số có tử bằng 1 và mẫu khác nhau
\(\eqalign{
& {7 \over {10}} = {5 \over {10}} + {2 \over {10}} = {1 \over 2} + {1 \over 5} \cr
& {{10} \over {21}} = {7 \over {21}} + {3 \over {21}} = {1 \over 3} + {1 \over 7} \cr
& {7 \over 8} = {4 \over 8} + {2 \over 8} + {1 \over 8} = {1 \over 2} + {1 \over 4} + {1 \over 8} \cr} \)
Câu 119: Tính một cách hợp lý
a) \({\rm{4}}{3 \over 4} + \left( { – 0,37} \right) + {1 \over 8} + \left( { – 1,28} \right) + \left( { – 2,5} \right) + 3{1 \over {12}}\)
b) \({3 \over {5.7}} + {3 \over {7.9}} + .. + {3 \over {59.61}}\)
c) \({{{5 \over {22}} + {3 \over {13}} – {1 \over 2}} \over {{4 \over {13}} – {2 \over {11}} + {3 \over 2}}}\)
a) \({\rm{4}}{3 \over 4} + \left( { – 0,37} \right) + {1 \over 8} + \left( { – 1,28} \right) + \left( { – 2,5} \right) + 3{1 \over {12}}\)
\(\eqalign{
& = \left( {4{3 \over 9} + {1 \over 8} + 3{1 \over {12}}} \right) – \left( {0,37 + 1,28 + 2,5} \right) \cr
& = \left( {4{{18} \over {24}} + {3 \over {24}} + 3{2 \over {24}}} \right) – \left( {4,15} \right) \cr
& = 7{{23} \over {24}} – 4{3 \over {20}} = 7{{115} \over {120}} – 4{{18} \over {120}} = 3{{97} \over {120}} \cr} \)
\(\eqalign{
& b){3 \over {5.7}} + {3 \over {7.9}} + .. + {3 \over {59.61}} \cr
& = {3 \over 2}.\left( {{2 \over {5.7}} + {2 \over {7.9}} + .. + {2 \over {59.61}}} \right) \cr
& = {3 \over 2}.\left( {{1 \over 5} – {1 \over 7} + {1 \over 7} – {1 \over 9} + … + {1 \over {59}} – {1 \over {61}}} \right) \cr
& = {3 \over 2}.\left( {{1 \over 5} – {1 \over {61}}} \right) \cr
& = {3 \over 2}.{{56} \over {305}} = {{84} \over {305}} \cr} \)
\(\eqalign{
& c){{{5 \over {22}} + {3 \over {13}} – {1 \over 12}} \over {{4 \over {13}} – {2 \over {11}} + {3 \over 2}}} = {{\left( {{5 \over {22}} + {3 \over {13}} – {1 \over 12}} \right).\left( {2.11.13} \right)} \over {\left( {{4 \over {13}} – {2 \over {11}} + {3 \over 2}} \right).\left( {2.11.13} \right)}} \cr
& = {{65 + 66 – 143} \over {88 – 52 + 429}} = {{ – 12} \over {465}} = {{ – 4} \over {155}} \cr} \)

