Bài 34: Chứng minh rằng:
a) \({{1 – 2\sin \alpha \,\cos \alpha } \over {{{\cos }^2}\alpha – {{\sin }^2}\alpha }} = {{1 – \tan \alpha } \over {1 + \tan \alpha }}\) khi các biểu thức đó có nghĩa
b) \(ta{n^2}\alpha {\rm{ }} – {\rm{ }}si{n^2}\alpha {\rm{ }} = {\rm{ }}ta{n^2}\alpha {\rm{ }}si{n^2}\alpha \)
c) \(2(1{\rm{ }}-\sin\alpha {\rm{ }})\left( {1{\rm{ }} + {\rm{ }}cos\alpha } \right){\rm{ }} = {\rm{ }}{\left( {1{\rm{ }} – {\rm{ }}\sin\alpha {\rm{ }} + {\rm{ }}\cos\alpha {\rm{ }}} \right)^2}\)
Đáp án
a) Ta có:
\(\eqalign{
& {{1 – 2\sin \alpha \,\cos \alpha } \over {{{\cos }^2}\alpha – {{\sin }^2}\alpha }} = {{{{(cos\alpha – \sin \alpha )}^2}} \over {(cos\alpha – \sin \alpha )(cos\alpha + \sin \alpha )}} \cr
& = {{(cos\alpha – \sin \alpha )} \over {(cos\alpha + \sin \alpha )}} = {{\cos \alpha (1 – \tan \alpha )} \over {\cos \alpha (1 + tan\alpha )}} \cr
& = {{1 – \tan \alpha } \over {1 + \tan \alpha }} \cr} \)
b) Ta có:
\(ta{n^2}\alpha {\rm{ }} – {\rm{ }}si{n^2}\alpha {\rm{ }} = {\rm{ }}ta{n^2}\alpha ({\rm{ }}1 – {\rm{ }}co{s^2}\alpha ){\rm{ }} = {\rm{ }}ta{n^2}\alpha {\rm{ }}si{n^2}\alpha \)
c) Ta có:
\(2(1-si{n}\alpha {\rm{ }})\left( {1{\rm{ }} + {\rm{ }}cos\alpha } \right){\rm{ }}\)
\(= {\rm{ }}2{\rm{ }}-{\rm{ }}2sin\alpha {\rm{ }} + {\rm{ }}2cos\alpha {\rm{ }}-{\rm{ }}2sin\alpha {\rm{ }}cos\alpha \)
\( = {\rm{ }}1{\rm{ }} + {\rm{ }}si{n^2}\alpha {\rm{ }} + {\rm{ }}co{s^2}\alpha {\rm{ }}-{\rm{ }}2sin\alpha {\rm{ }} + {\rm{ }}2cos\alpha {\rm{ }} \)
\(- {\rm{ }}2sin\alpha {\rm{ }}cos\alpha \)
\( = {\rm{ }}{\left( {1{\rm{ }} – {\rm{ }}sin\alpha {\rm{ }} + {\rm{ }}cos\alpha {\rm{ }}} \right)^2}\)
Bài 35: Biết \(\sinα -\cosα =m\), hãy tính \(si{n^3}\alpha {\rm{ }} – {\rm{ }}co{s^3}\alpha \)
Đáp án
Advertisements (Quảng cáo)
Ta có:
\(si{n^3}\alpha {\rm{ }} – {\rm{ }}co{s^3}\alpha \)
\( = {\rm{ }}\left( {sin\alpha {\rm{ }}-{\rm{ }}cos\alpha } \right)(si{n^2}\alpha {\rm{ }} + {\rm{ }}sin\alpha {\rm{ }}cos\alpha {\rm{ }} + {\rm{ }}co{s^2}\alpha )\)
\(= m(1 + sinα cosα)\) (1)
Từ \(\sinα – \cosα = m ⇒ 1 – 2\sinα \cosα = m^2\)
⇒ \(\sin \alpha \,\cos \alpha = {{1 – {m^2}} \over 2}\,\,\,\,\,\,\,(2)\)
Thay (2) vào (1) ta được:
\({\sin ^3}\alpha – {\cos ^3}\alpha = m(1 + {{1 – {m^2}} \over 2}) = {m \over 2}(3 – {m^2})\)
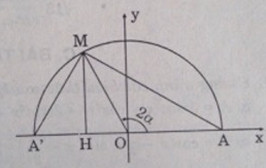
Bài 36: Với số \(α,0 < \alpha < {\pi \over 2}\) , xét điểm M của đường tròn lượng giác xác định bởi 2α , rồi xét tam giác vuông A’MA (A’ đối xứng với A qua tâm O của đường tròn).
a) Tính AM2 bằng hai cách khác nhau để suy ra: cos2α = 1 – 2sin2α
Advertisements (Quảng cáo)
b) Tính diện tích tam giác A’MA bằng hai cách khác nhau để suy ra: sin2α = 2sinα cosα
c) Chứng minh: \(\sin {\pi \over 8} = {1 \over 2}\sqrt {2 – \sqrt 2 } ;\,\,\,\cos {\pi \over 8} = {1 \over 2}\sqrt {2 + \sqrt 2 } \) rồi tính các giá trị lượng giác của các góc \({{3\pi } \over 8}\) và \({{5\pi } \over 8}\)
Đáp án
a) Ta có:
\(\eqalign{
& A{M^2} = \overline {AH} .\overline {{\rm{AA}}} {\rm{‘ = (}}\overline {AO} + \overline {OH} ).\overline {{\rm{AA}}’} \cr
& = ( – 1 + \cos 2\alpha )( – 2) = 2(1 – \cos 2\alpha ) \cr} \)
Lại có: \(A{M^2} = A{A^2}.si{n^2}\alpha = 4si{n^2}\alpha \)
Vậy: \(2si{n^2}\alpha = 1-cos2\alpha \)
b) Ta có: \({S_{A’MA}} = {1 \over 2}AA’.MH = MH = \sin 2\alpha \)
Lại có:
\({S_{A’MA}} = {1 \over 2}A’M.AM = {1 \over 2}A’A\cos \alpha .A’A\sin \alpha \)
\(= 2\sin \alpha \cos \alpha \)
Vậy: \(\sin2α = 2\sinα \cosα\)
c) Ta có: \(\cos {\pi \over 4} = 1 – 2{\sin ^2}{\pi \over 8}\) nên:
\(\eqalign{
& {\sin ^2}{\pi \over 8} = {1 \over 2}(1 – {{\sqrt 2 } \over 2}) = {{2 – \sqrt 2 } \over 4} \cr
& \sin {\pi \over 8} = {{\sqrt {2 – \sqrt 2 } } \over 2} \cr
& \cos {\pi \over 4} = 2{\cos ^2}{\pi \over 8} – 1 \cr&\Rightarrow {\cos ^2}{\pi \over 8} = {1 \over 2}(1 + {{\sqrt 2 } \over 2}) = {{2 + \sqrt 2 } \over 4} \cr
& \cos {\pi \over 8} = {{\sqrt {2 + \sqrt 2 } } \over 2} \cr
& {{3\pi } \over 8} = {\pi \over 2} – {\pi \over 8} \Rightarrow \left\{ \matrix{
\cos {{3\pi } \over 8} = \sin {\pi \over 8} = {{\sqrt {2 – \sqrt 2 } } \over 2} \hfill \cr
\sin {{3\pi } \over 8} = \cos {\pi \over 8} = {{\sqrt {2 + \sqrt 2 } } \over 2} \hfill \cr
\tan {{3\pi } \over 8} = \cot {\pi \over 8} = \sqrt 2 + 1 \hfill \cr
\cot {{3\pi } \over 8} = \tan {\pi \over 8} = \sqrt 2 – 1 \hfill \cr} \right. \cr
& {{5\pi } \over 8} = {\pi \over 2} + {\pi \over 8} \Rightarrow \left\{ \matrix{
\cos {{5\pi } \over 8} = – \sin {\pi \over 8} = {{\sqrt {2 – \sqrt 2 } } \over 2} \hfill \cr
\sin {{5\pi } \over 8} = \cos {\pi \over 8} = {{\sqrt {2 + \sqrt 2 } } \over 2} \hfill \cr
\tan {{5\pi } \over 8} = – \cot {\pi \over 8} = – \sqrt 2 – 1 \hfill \cr
\cot {{5\pi } \over 8} = – \tan {\pi \over 8} = 1 – \sqrt 2 \hfill \cr} \right. \cr} \)
Bài 37: Trong hệ tọa độ vuông góc Oxy gắn với một đường tròn lượng giác, cho điểm P có tọa độ (2, -3)
a) Chứng minh rằng điểm M sao cho \(\overrightarrow {OM} = {{\overrightarrow {OP} } \over {|\overrightarrow {OP} |}}\) là giao điểm của tia OP với đường tròn lượng giác đó
b) Tính tọa độ điểm M và từ đó suy ra cosin, sin của góc lượng giác (Ox, OP)
Đáp án
a) Ta có:
\(\left\{ \matrix{
\overrightarrow {OM} \uparrow \uparrow \overrightarrow {OP} \hfill \cr
|\overrightarrow {OM} | = |{{\overrightarrow {OP} } \over {\overrightarrow {OP} }}| = {{|\overrightarrow {OP} |} \over {|\overrightarrow {OP} |}}=1 \hfill \cr} \right. \)
Vậy M là giao của tia OP với đường tròn lượng giác.
b) Ta có:
\(\eqalign{
& |\overrightarrow {OP} |\, = \sqrt {{2^2} + {{( – 3)}^2}} = \sqrt {13} \cr
& \Rightarrow \overrightarrow {OM} ({2 \over {\sqrt {13} }};\, – {3 \over {\sqrt {13} }}) \cr} \)
Vậy
\(\left\{ \matrix{
\cos (Ox,OP) = {2 \over {\sqrt {13} }} \hfill \cr
sin(Ox,OP) = {{ – 3} \over {\sqrt {13} }} \hfill \cr} \right.\)

