Câu 6: Phát biểu mệnh đề đảo của nguyên lí “ Trong một tam giác cân, hai đường cao ứng với hai cạnh bên bằng nhau”. Mệnh đề đảo đó đúng hay sai?
Mệnh đề đảo là: “Trong một tam giác, hai đường cao ứng với hai cạnh bên bằng nhau thì tam giác đó cân”. Mệnh đề đảo đúng.
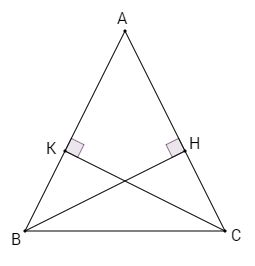
Ví dụ: giả sử hai đường cao BK = CK
Ta có:
\(\eqalign{
& {S_{ABC}} = {1 \over 2}.BH.AC = {1 \over 2}.CK.AB \cr
& \Rightarrow AC = AB \cr} \)
Advertisements (Quảng cáo)
Vậy tam giác ABC cân tại A.
Câu 7: Chứng minh định lý sau bằng phản chứng:
“Nếu a, b là hai số dương thì \(a + b \ge 2\sqrt {ab} \)
Advertisements (Quảng cáo)
Giả sử: \(a + b < 2\sqrt {ab} \) .
Ta có:
\(a + b – 2\sqrt {ab} < 0 \Rightarrow {(\sqrt a – \sqrt b )^2} < 0\) (vô lý)
Vậy \(a + b \ge 2\sqrt {ab} \)
Câu 8: Sử dụng thuật ngữ “điều kiện đủ” để phát biểu định lý “Nếu a và b là hai số hữu tỉ thì tổng a + b cũng là số hữu tỉ”.
“a và b là hai số hữu tỉ là điều kiện đủ để tổng a + b cũng là số hữu tỉ”
Câu 9: Sử dụng thuật ngữ “điều kiện cần” để phát biểu định lý “ Nếu một số tự nhiên chia hết cho 15 thì nó chia hết cho 5”.
“Một số chia hết cho 5 là điều kiện cần để nó chia hết cho 15.”

