Bài 9: Cho tam giác ABC có \(a = 12,\,b = 16,\,c = 20\). Tính diện tích S, chiều cao \(h_a\), các bán kính R, r của đường tròn ngoại tiếp, nội tiếp tam giác đó.

Ta có \(p = {{a + b + c} \over 2} = {{12 + 16 + 20} \over 2} = 24\)
Áp dụng công thức Hêrông, ta có
\(\eqalign{
& S = \sqrt {p(p – a)(p – b)(p – c)} = \sqrt {24.12.8.4} = 96 \cr
& S = {1 \over 2}a.{h_a}\,\,\, \Rightarrow {h_a} = {{2S} \over a} = {{2.96} \over {12}} = 16 \cr
& S = {{abc} \over {4R}}\,\,\,\,\,\, \Rightarrow \,R = {{abc} \over {4S}} = {{12.16.20} \over {4.96}} = 10 \cr
& S = pr\,\,\,\,\,\,\,\, \Rightarrow \,r = {S \over p} = {{96} \over {24}} = 4 \cr} \)
Bài 10: Cho tam giác ABC. Chứng minh rằng
a)\(\cot A = {{{b^2} + {c^2} – {a^2}} \over {4S}}\) ( S là diện tích tam giác ABC) ;
b) \(\cot A + \cot B + \cot C = {{{a^2} + {b^2} + {c^2}} \over {4S}}\).

a) Ta có
Advertisements (Quảng cáo)
\(\eqalign{
& \,\,\,\,\,\,\cos A = {{{b^2} + {c^2} – {a^2}} \over {2bc}}\,\,;\,\,\,\,S = {1 \over 2}bc.\sin A \cr
& \Rightarrow \,\,\cot A = {{\cos A} \over {\sin A}} = {{{b^2} + {c^2} – {a^2}} \over {2bc.\sin A}} = {{{b^2} + {c^2} – {a^2}} \over {4S}} \cr} \)
b) Tương tự câu a), ta có
\(\eqalign{
& \,\,\cot B = {{{a^2} + {c^2} – {b^2}} \over {4S}}\,\,;\,\,\,\,\cot C = {{{a^2} + {b^2} – {c^2}} \over {4S}} \cr
& \Rightarrow \,\,\cot A + \cot B + \cot C\cr& = {{{b^2} + {c^2} – {a^2}} \over {4S}} + {{{a^2} + {c^2} – {b^2}} \over {4S}} + {{{a^2} + {b^2} – {c^2}} \over {4S}} \cr
& = \,{{{a^2} + {b^2} + {c^2}} \over {4S}} \cr} \)
Bài 11: Cho hai đường tròn \((O\,;\,R)\) và \(({O’}\,;\,{R’})\) cắt nhau tại hai điểm A và B. Trên đường thẳng AB, lấy điểm C ở ngoài hai đường tròn và kẻ hai tiếp tuyến CE, CF đến hai đường tròn đó ( E, F là các tiếp điểm). Chứng minh rằng CE = CF.

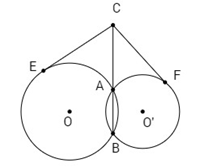
Advertisements (Quảng cáo)
Ta có
\(\eqalign{
& \,\,\,\,\,{\wp _{{C_{/(O)}}}} = CA.CB = C{E^2} \cr
& \,\,\,\,\,{\wp _{{C_{/({O\,’})}}}} = CA.CB = C{F^2} \cr
& \Rightarrow \,\,\,CE = CF \cr} \)
Bài 12: Cho đường tròn (O; R) và một điểm P cố định ở bên trong đường tròn đó. Hai dây cung thay đổi AB và CD luôn đi qua P và vuông góc với nhau.
a) Chứng minh rằng \(A{B^2} + C{D^2}\) không đổi.
b) Chứng minh rằng \(P{A^2} + P{B^2} + P{C^2} + P{D^2}\) không phụ thuộc vào vị trí của điểm P.

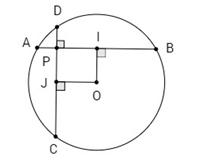
a) Gọi I, J lần lượt là trung điểm của AB, CD.
Ta có \(OI \bot AB\,\,;\,\,OJ \bot CD\)
Suy ra OIPJ là hình chữ nhật. Ta có
\(\eqalign{
& A{B^2} + C{D^2} = 4(A{I^2} + C{J^2}) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 4(O{A^2} – O{I^2} + C{O^2} – J{O^2}) \cr} \)
\( = 4(2{R^2} – O{P^2})\) ( không đổi do cố định).
b) Ta có
\(\eqalign{
& P{A^2} + P{B^2} + P{C^2} + P{D^2} \cr&= {(\overrightarrow {PA} – \overrightarrow {PB} )^2} + {(\overrightarrow {PC} – \overrightarrow {PD} )^2} + 2.\overrightarrow {PA} .\,\overrightarrow {PB} + 2\overrightarrow {PC} .\,\overrightarrow {PD} \cr
& = A{B^2} + C{D^2} + 4(P{O^2} – {R^2}) \cr
& = 4(2{R^2} – O{P^2}) + 4(P{O^2} – {R^2}) \cr
& = 4{R^2} \cr} \)
Vậy \(P{A^2} + P{B^2} + P{C^2} + P{D^2}\) không phụ thuộc vào vị trí của điểm P

