Bài 2.45: Cho tam giác ABC thỏa mãn điều kiện \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB} – \overrightarrow {AC} } \right|\). Vậy tam giác ABC là tam giác gì?

(h.2.32)
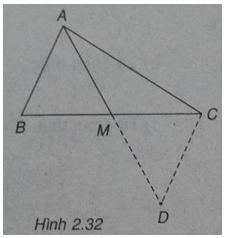
Gọi M là trung điểm của cạnh BC ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} = \overrightarrow {AD} \)
Mặt khác \(\overrightarrow {AB} – \overrightarrow {AC} = 2\overrightarrow {CB} \). Theo giả thiết ta có:
\(\left| {2\overrightarrow {AM} } \right| = \left| {\overrightarrow {CB} } \right| = \left| {\overrightarrow {AD} } \right|\)
Advertisements (Quảng cáo)
Hay \(AM = {{BC} \over 2}\)
Ta suy ra ABC là tam giác vuông tại A.
Bài 2.46: Ba điểm A, B, C phân biệt tạo nên vec tơ \(\overrightarrow {AB} + \overrightarrow {AC} \) vuông góc với vec tơ \(\overrightarrow {AB} + \overrightarrow {CA} \). Vậy tam giác ABC là tam giác gì?

Theo giả thiết ta có:
Advertisements (Quảng cáo)
\(\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\left( {\overrightarrow {AB} + \overrightarrow {CA} } \right) = 0\)
\(\eqalign{
& \Leftrightarrow \left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\left( {\overrightarrow {AB} – \overrightarrow {AC} } \right) = 0 \cr
& \Leftrightarrow {\overrightarrow {AB} ^2} – \overrightarrow {AC} {}^2 = 0 \cr} \)
Ta suy ra ABC là tam giác có AB = AC (tam giác cân tại A)
Bài 2.47: Tính các cạnh còn lại của tam giác ABC trong mỗi trường hợp sau:
a) \(a = 7,b = 10,\widehat C = {56^0}29’\)
b) \(a = 2,c = 3,\widehat B = {123^0}17’\)
c) \(b = 0,4,c = 12,\widehat A = {23^0}28’\)
 a) \(\eqalign{
a) \(\eqalign{
& {c^2} = {a^2} + {b^2} – 2ab\cos C \cr
& = 49 + 100 – 140\cos {56^0}29′ \cr} \)
=> \({c^2} \approx 71,7\) hay \(c \approx 8,47\)
b) \(b \approx 4,43\)
c) \(a \approx 11,63\)

