Bài 2.65: Trong mặt phẳng tọa độ cho ba điểm A(7; – 3), B(8;4), C(1;5).
a) Tìm tọa độ điểm D thỏa mãn \(\overrightarrow {AB} = \overrightarrow {DC} \);
b) Chứng minh rằng tứ giác ABCD là hình vuông.

a) \(\overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \left\{ \matrix{
8 – 7 = 1 – {x_D} \hfill \cr
4 + 3 = 5 – {y_D} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{x_D} = 0 \hfill \cr
{y_D} = – 2 \hfill \cr} \right.\)
Vậy D(0;-2)
b) Ta có: \(\overrightarrow {AB} = \overrightarrow {DC} \,(1)\)
\(\overrightarrow {AB} = (1;7),\overrightarrow {AD} = ( – 7;1)\)
\(\overrightarrow {AB} .\overrightarrow {AD} = – 7 + 7 = 0\,(2)\)
\(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {AD} } \right| = \sqrt {1 + 49} = 5\sqrt 2 \,(3)\)
Từ (1), (2), (3) =>ABCD là hình vuông.
Bài 2.66: Trên mặt phẳng tọa độ Oxy cho hai điểm A(1;3) và B(4;2).
a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB;
Advertisements (Quảng cáo)
b) Tính chu vi tam giác OAB;
c) Tính diện tích tam giác OAB.

a) Vì điểm D nằm trên Ox nên tọa độ của nó có dạng D(x;0)
Theo giả thiết DA = DB nên \(D{A^2} = D{B^2}\)
Do đó:
\({(1 – x)^2} + {3^2} = {(4 – x)^2} + {2^2}\)
\(\eqalign{
& \Leftrightarrow {x^2} – 2x + 1 + 9 = {x^2} – 8x + 16 + 4 \cr
& \Leftrightarrow x = {5 \over 3} \cr} \)
Advertisements (Quảng cáo)
Vậy điểm D có tọa độ \(\left( {{5 \over 3};0} \right)\)
b) Gọi 2p là chu vi tam giác OAB, ta có:
\(\eqalign{
& 2p = OA + OB + OC \cr
& = \sqrt {{1^2} + {3^2}} + \sqrt {{4^2} + {2^2}} + \sqrt {{3^2} + {1^2}} \cr
& = \sqrt {10} + \sqrt {20} + \sqrt {10} \cr
& = \sqrt {10} (2 + \sqrt 2 ) \cr} \)
c) Ta có : \(O{A^2} + A{B^2} = O{B^2}\)
=> tam giác OAB vuông tại A
=> \({S_{OAB}} = {1 \over 2}OA.AB = {1 \over 2}\sqrt {10} .\sqrt {10} = 5\)
Vậy diện tích tam giác OAB là 5 (đvdt)
Bài 2.67: Trên mặt phẳng tọa độ Oxy cho điểm A(2;-1)
a)Tìm tọa độ điểm B đối xứng với A qua gốc tọa độ O;
b) Tìm tọa độ điểm C có tung độ bằng 2 sao cho tam giác ABC vuông ở C.

(Xem hình 2.36)
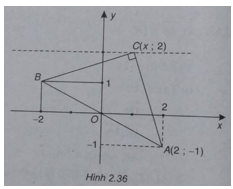
a) Ta có A(2;-1), tọa độ điểm B đối xứng với A qua O là B(-2;1)
b) Ta có: C(x;2), do đó:
\(\eqalign{
& \overrightarrow {CB} = ( – 2 – x; – 1); \cr
& \overrightarrow {CA} = (2 – x; – 3) \cr} \)
Tam giác ABC vuông tại C nên
\(\eqalign{
& \overrightarrow {CA} .\overrightarrow {CB} = 0 \cr
& \Leftrightarrow ( – 2 – x)(2 – x) + 3 = 0 \cr
& \Leftrightarrow {x^2} = 1 \cr
& \Leftrightarrow x = \pm 1 \cr} \)
Vậy ta có hai điểm C(1;2) và (-1;2).

