Bài 2 Tích vô hướng của hai vecto Sách bài tập Toán Hình học 10. Giải bài 2.17, 2.18, 2.19, 2.20 trang 91, 92 Sách bài tập Toán Hình học 10. Câu 2.17: Tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 11 cm…
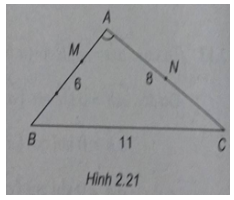
Bài 2.17: Tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 11 cm.
a) Tính \(\overrightarrow {AB} .\overrightarrow {AC} \) và chứng tỏ rằng tam giác ABC có góc A tù.
b) Trên cạnh AB lấy điểm M sao cho AM = 2 cm và gọi N là trung điểm của cạnh AC. Tính \(\overrightarrow {AM} .\overrightarrow {AN} \).

(h.2.21)
a) \(\eqalign{
& \overrightarrow {AB} .\overrightarrow {AC} = {1 \over 2}(A{C^2} + A{B^2} – B{C^2}) \cr
& = {1 \over 2}({8^2} + {6^2} – {11^2}) = – {{21} \over 2} \cr} \)
\( = AB.AC.cosA = – {{21} \over 2}\)
=> Góc A tù
b) Ta có:
\(\overrightarrow {AM} = {1 \over 3}\overrightarrow {AB} ,\overrightarrow {AN} = {1 \over 2}\overrightarrow {AC} \)
Do đó:
\(\eqalign{
& \overrightarrow {AM.} \overrightarrow {AN} = {1 \over 3}\overrightarrow {AB} .{1 \over 2}\overrightarrow {AC} \cr
& = {1 \over 6}\overrightarrow {AB} .\overrightarrow {AC} = {1 \over 6}.( – {{21} \over 2}) = – {7 \over 4} \cr}\)
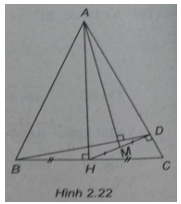
Bài 2.18: Cho tam giác ABC cân (AB = AC). Gọi H là trung điểm của cạnh BC, D là hình chiếu vuông góc của H trên cạnh AC, M là trung điểm của đoạn HD. Chứng minh rằng AM vuông góc với BD.

(h.2.22)
Ta cần chứng minh \(\overrightarrow {AM} .\overrightarrow {BD} = 0\)
Advertisements (Quảng cáo)
Tac có: \(2\overrightarrow {AM} = \overrightarrow {AH} + \overrightarrow {AD} \) vì M là trung điểm của đoạn HD.
\(\overrightarrow {BD} = \overrightarrow {BH} + \overrightarrow {HD} \)
Do đó:
\(2\overrightarrow {AM} .\overrightarrow {BD} = (\overrightarrow {AH} + \overrightarrow {AD} ).(\overrightarrow {BH} + \overrightarrow {HD} )\)
\(= \underbrace {\overrightarrow {AH} .\overrightarrow {BH} }_{ = 0} + \overrightarrow {AH} .\overrightarrow {HD} + \overrightarrow {AD} .\overrightarrow {BH} + \underbrace {\overrightarrow {AD} .\overrightarrow {HD} }_{ = 0}\)
\( = > \,2\overrightarrow {AM} .\overrightarrow {BD} = \overrightarrow {AH} .\overrightarrow {HD} + \overrightarrow {AD} .\overrightarrow {BH} \)
\( = (\overrightarrow {AH} .\overrightarrow {HD} + (\overrightarrow {AH} + \overrightarrow {HD} ).\overrightarrow {BH} \)
\( = \overrightarrow {AH} .\overrightarrow {HD} + \underbrace {\overrightarrow {AH} .\overrightarrow {BH} }_{ = 0} + \overrightarrow {HD} .\overrightarrow {BH} \)
\( = \overrightarrow {HD} .(\underbrace {\overrightarrow {AH} .\overrightarrow {BH} }_{\overrightarrow {AC} }) = \overrightarrow {HD} .\overrightarrow {AC} = 0\)
Vậy AM vuông góc với BD.
Advertisements (Quảng cáo)
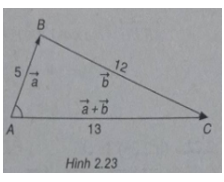
Bài 2.19: Cho hai véc tơ \(\overrightarrow a \) và \(\overrightarrow b \) có \(\left| {\overrightarrow a } \right| = 5,\left| {\overrightarrow b } \right| = 12\) và \(\left| {\overrightarrow a + \overrightarrow b } \right| = 13\). Tính tích vô hướng \(\overrightarrow a .(\overrightarrow a + \overrightarrow b )\) và suy ra góc giữa hai vec tơ \(\overrightarrow a \) và \(\overrightarrow a + \overrightarrow b \)

(h.2.23)
Dựng tam giác ABC có AB = 5, BC= 12 và AC = 13.
Ta có \(\left| {\overrightarrow a } \right| = 5,\left| {\overrightarrow b } \right| = 12\) và \(\left| {\overrightarrow a + \overrightarrow b } \right| = 13\)
Và \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow a + \overrightarrow b \)
Khi đó \(\overrightarrow a (\overrightarrow a + \overrightarrow b ) = \overrightarrow {AB} .\overrightarrow {AC} \)
Mặt khác ta có:
\(\overrightarrow {AB} .\overrightarrow {AC} = {1 \over 2}(A{C^2} + A{B^2} – B{C^2})\)
\( = {1 \over 2}({13^2} + {5^2} – {12^2}) = 25\)
Ta suy ra:
\(\eqalign{
& \cos (\overrightarrow {AB} .\overrightarrow {AC} ) = {{\overrightarrow {AB} .\overrightarrow {AC} } \over {\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} \cr
& = {{25} \over {5.13}} \approx 0,3846 \cr} \)
Suy ra \((\overrightarrow {AB} .\overrightarrow {AC} ) \approx {67^0}23’\)
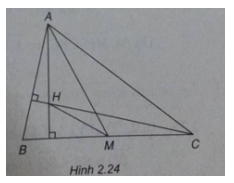
Bài 2.20: Cho tam giác ABC. Gọi H là trực tâm của tam giác và M là trung điểm của cạnh BC. Chứng minh rằng \(\overrightarrow {MH} .\overrightarrow {MA} = {1 \over 4}B{C^2}\)

(h.2.24)
Ta có \(\overrightarrow {AM} = {1 \over 2}(\overrightarrow {AB} + \overrightarrow {AC} )\)
\(\overrightarrow {HM} = {1 \over 2}(\overrightarrow {HB} + \overrightarrow {HC} )\)
\( = > \overrightarrow {AM} .\overrightarrow {HM} = {1 \over 4}(\overrightarrow {AB} + \overrightarrow {AC} ).(\overrightarrow {HB} + \overrightarrow {HC} )\)
\( = {1 \over 4}(\overrightarrow {AB} .\overrightarrow {HB} + \underbrace {\overrightarrow {AB} .\overrightarrow {HC} }_{ = 0} + \underbrace {\overrightarrow {AC} \overrightarrow {.HB} }_{ = 0} + \overrightarrow {AC} .\overrightarrow {HC} )\)
\( = {1 \over 4}(\overrightarrow {AB} .\overrightarrow {HB} + \overrightarrow {AC} .\overrightarrow {HC} )\)
\( = {1 \over 4}\left[ {\overrightarrow {AB} .(\overrightarrow {HC} + \overrightarrow {CB} ) + \overrightarrow {AC} .(\overrightarrow {HB} + \overrightarrow {BC} )} \right]\)
\( = {1 \over 4}\left[ {\underbrace {\overrightarrow {AB} .\overrightarrow {HC} }_0 + \overrightarrow {AB} .\overrightarrow {CB} + \underbrace {\overrightarrow {AC} .\overrightarrow {HB} }_0 + \overrightarrow {AC} .\overrightarrow {BC} } \right]\)
\( = {1 \over 4}(\overrightarrow {AB} .\overrightarrow {CB} + \overrightarrow {AC} .\overrightarrow {BC} ) = {1 \over 4}(\overrightarrow {AB} .\overrightarrow {CB} – \overrightarrow {AC} .\overrightarrow {CB} )\)
\( = {1 \over 4}\overrightarrow {CB} .(\underbrace {\overrightarrow {AB} – \overrightarrow {AC} }_{\overrightarrow {CB} }) = {1 \over 4}{\overrightarrow {CB} ^2} = {1 \over 4}{\overrightarrow {BC} ^2}\)

