Bài 65: Tìm a và b để bất phương trình
\((x – 2a + b – 1)(x + a – 2b + 1) \le 0\)
Có tập nghiệm là đoạn [0;2].

Tập nghiệm của bất phương trình đã cho là đoạn \({\rm{[}}2a – b + 1; – a + 2b – 1]\) (nếu \(2a – b + 1 \le – a + 2b – 1\)) hoặc là đoạn \({\rm{[}} – a + 2b – 1;2a – b + 1]\) (nếu \( – a + 2b – 1 \le 2a – b – 1\))
Do đó để tập nghiệm của bất phương trình đã cho là đoạn [0;2], điều kiện cần và đủ là:
\((1)\,\left\{ \matrix{
2a – b + 1 = 2 \hfill \cr
– a + 2b – 1 = 0 \hfill \cr} \right.\)
hoặc
\((2)\,\left\{ \matrix{
2a – b + 1 = 0 \hfill \cr
– a + 2b – 1 = 2. \hfill \cr} \right.\)
Giải (1) ta được a = b = 1. Giải hệ (2) ta được \(a = {1 \over 3},b = {5 \over 3}\)
Đáp số: a = b = 1 hoặc \(a = {1 \over 3},b = {5 \over 3}\)
Bài 66: Tìm a và b (b > -1) để hai bất phương trình sau tương đương
\((x – a + b)(x + 2a – b – 1) \le 0\) (1)
Và \(\left| {x + a – 2} \right| \le b + 1.\) (2)
Advertisements (Quảng cáo)

(1) \( \Leftrightarrow x \in {\rm{[}}\alpha ;\beta {\rm{]}}\), trong đó
\(\left\{ \matrix{
\alpha = a – b \hfill \cr
\beta = – 2a + b + 1 \hfill \cr} \right.\)
hoặc
\(\left\{ \matrix{
\alpha = – 2a + b + 1 \hfill \cr
\beta = a – b. \hfill \cr} \right.\)
(2) \( \Leftrightarrow – (b + 1) \le x + a – 2 \le b + 1\)
\(\Leftrightarrow – b – a + 1 \le x \le – a + b + 3\)
\(\Leftrightarrow x \in {\rm{[}} – b – a + 1; – a + b + 3]\)
Advertisements (Quảng cáo)
(1) và (2) tương đương khi và chỉ khi \({\rm{[}}\alpha ;\beta {\rm{]}} = {\rm{[}} – b – a + 1; – a + b + 3]\), tức là:
\(\left\{ \matrix{
\alpha = – b – a + 1 \hfill \cr
\beta = – a + b + 3 \hfill \cr} \right.\)
\( \Leftrightarrow (3)\left\{ \matrix{
a – b = – b – a + 1 \hfill \cr
– 2a + b + 1 = – a + b + 3 \hfill \cr} \right.\)
hoặc
\(\left\{ \matrix{
– 2a + b + 1 = – b – a + 1 \hfill \cr
a – b = – a + b + 3 \hfill \cr} \right.\)
Hệ phương trình (3) vô nghiệm. Hệ phương trình (4) có nghiệm duy nhất \(a = 3,b = {3 \over 2}\)
Đáp số: \(a = 3,b = {3 \over 2}\).
Bài 67: a) Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau
\(y = f(x) = \left| {x + 3} \right| – 1\);
\(y = g(x) = \left| {2x – m} \right|\); trong đó m là tham số
Xác định hoành độ các giao điểm của mỗi đồ thị với trục hoành.
b) Tìm các giá trị của tham số m để bất phương trình sau nghiệm đúng với mọi giá trị của x
\(\left| {2x – m} \right| > \left| {x + 3} \right| – 1\)

a) Đồ thị hàm số y = f(x) là đường gấp khúc u’Eu, cắt Ox tại A(-4; 0) và B(-2;0).
Đồ thị hàm số y = g(x) là đường gấp khúc v’Cv, cắt Ox tại \(C({m \over 2};0)\)
Khi m thay đổi, điểm C chạy trên Ox; tia Cv luông song song với đường thẳng y = 2x; tia Cv’ luôn song song với đường thẳng y = -2x.
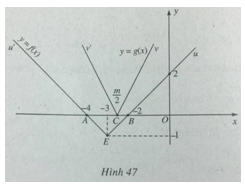
b) Bất phương trình đã cho đúng với mọi x khi và chỉ khi đồ thị của hàm số y = g(x) nằm hoàn toàn phía trên đồ thị của hàm số y = f(x) hay C nằm giữa A và B nghĩa là \( – 4 < {m \over 2} < – 2 \Leftrightarrow – 8 < m < – 4\)
Đáp số: \( – 8 < m < – 4\)

