Bài 31.15: Một người đứng tuổi nhìn rõ được các vật ở xa. Muốn nhìn rõ vật gần nhất cách mắt 27 cm thì phải đeo kính + 2,5 dp cách mắt 2 cm.
a) Xác định các điểm Cc và Cv của mắt.
b) Nếu đeo kính sát mắt thì có thể nhìn rõ các vật ở trong khoảng nào ?
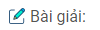
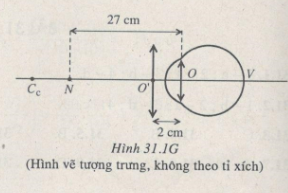
a) Vì CV–> ∞ \( \Rightarrow {f_k} = \frac{1}{{{D_k}}} = \frac{1}{{2,5}} = 0,4m = 40cm\)
Ta có: \(\begin{array}{l}
\frac{1}{{O’N}} – \frac{1}{{O'{C_C}}} = \frac{1}{{{f_k}}} \Rightarrow \frac{1}{{O'{C_C}}} = \frac{1}{{25}} – \frac{1}{{40}}\\
\Rightarrow O'{C_C} = \frac{{25.40}}{{40 – 25}} = \frac{{200}}{3}cm
\end{array}\)
Advertisements (Quảng cáo)
Vậy
\(O{C_C} = \frac{{200}}{3} + 2 = \frac{{206}}{3} \approx 68,6cm\)
b) Tiêu cự của thấu kính tương đương với hệ (mắt + kính):
\(\frac{1}{f} = \frac{1}{{{f_{mat}}}} + \frac{1}{{{f_k}}}\)
Advertisements (Quảng cáo)
Khoảng phải tìm giới hạn bởi M và N xác định như sau:
|
\(M\xrightarrow{{(mat + kinh)}}M’ \equiv V\) * Có kính: \(\frac{1}{{OM}} + \frac{1}{{OV}} = \frac{1}{{{f_{max}}}} + \frac{1}{{{f_k}}}\) * Không kính: \(\begin{gathered}
|
\(N\xrightarrow{{(mat + kinh)}}N’ \equiv V\) * Có kính: \(\frac{1}{{ON}} + \frac{1}{{OV}} = \frac{1}{{{f_{\min }}}} + \frac{1}{{{f_k}}}\) * Không kính: \(\begin{gathered} |
Bài 31.16: Mắt của một người cận thị có điểm Cv cách mắt 20 cm.
a) Để khắc phục tật này, người đó phải đeo kính gì, độ tụ bao nhiêu để nhìn rõ các vật ở xa vô cùng ?
b) Người này muốn đọc một thông báo cách mắt 40 cm nhưng không có kính cận mà lại sử dụng một thấu kính phân kì có tiêu cự 15 cm. Để đọc được thông báo trên mà không phải điều tiết thì phải đặt thấu kính phân kì cách mắt bao nhiêu ?
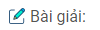
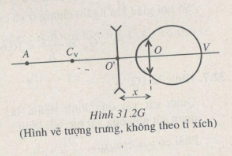
a) fk = -OCV = -20cm
Dk = 1/fk = -1/0,2 = -5 dp.
b) \(\begin{gathered}
\frac{1}{{O’A}} – \frac{1}{{O'{C_V}}} = \frac{1}{{f{‘_k}}} \hfill \\
\Rightarrow \frac{1}{{40 – x}} – \frac{1}{{20 – x}} = – \frac{1}{{15}} \hfill \\
\end{gathered} \)
 x = 10cm (Hình 31.2G)
x = 10cm (Hình 31.2G)

