Bài 1.6: a) Tính lực hút tĩnh điện giữa hạt nhân trong nguyên tử heli với một êlectron trong lớp vỏ nguyên tử. Cho rằng êlectron này nằm cách hạt nhân 2,94.10-11 m.
b) Nếu êlectron này chuyển động tròn đều quanh hạt nhân với bán kính quỹ đạo như đã cho ở trên thì tốc độ góc của nó sẽ là bao nhiêu ?
c) So sánh lực hút tĩnh điện với lực hấp dẫn giữa hạt nhân và êlectron.
Điện tích của êlectron : -1,6.10-19C. Khối lượng của êlectron : 9,1.10-31kg.
Khối lượng của hạt nhân heli 6,65.10-27kg. Hằng số hấp dẫn 6,67.1011 m3/kg.s2.
a) \(F = k{{\left| {{q_1}{q_2}} \right|} \over {{r^2}}} = {5,33.10^{ – 7}}N\)
b) \(F = k{{\left| {{q_1}{q_2}} \right|} \over {{r^2}}} = {5,33.10^{ – 7}}N\)
c) \(F = k{{\left| {{q_1}{q_2}} \right|} \over {{r^2}}} = {5,33.10^{ – 7}}N\)
Bài 1.7: Hai quả cầu nhỏ giống nhau bằng kim loại, có khối lượng 5 g, được treo vào cùng một điểm O bằng hai sợi chỉ không dãn, dài 10 cm. Hai quả cầu tiếp xúc với nhau. Tích điện cho một quả cầu thì thấy hai quả cầu đẩy nhau cho đến khi hai dây treo hợp với nhau một góc 600.
Tính điện tích mà ta đã truyền cho các quả cầu. Lấy g = 10 m/s2.
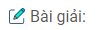
Điện tích q mà ta truyền cho các quả cầu sẽ phân bố đều cho hai quả cầu. Mỗi quả cầu mang một điện tích q/2. Hai quả cầu sẽ đẩy nhau với môt lực là
\(F = k{{{q^2}} \over {4{r^2}}}\)
Vì góc giữa hai dây treo α = 60° nên r = l= 10 cm. Mỗi quả cầu sẽ nằm cân bằng dưới tác dụng của ba lực: lực căng
\(\overrightarrow T \) của sợi dây, lực điện \(\overrightarrow F \) và trọng lực \(\overrightarrow P \) của quả cầu (Hình 1.1G)
Ta có:
\(\eqalign{
& \tan {\alpha \over 2} = {F \over P} = {{k{q^2}} \over {4{\ell ^2}mg}} \Rightarrow q = \pm 2\ell \sqrt {{{mg} \over k}\tan {\alpha \over 2}} \cr
& q \approx \pm {3,58.10^{ – 7}}C \cr} \)
Advertisements (Quảng cáo)
Bài 1.8: Một hệ điện tích có cấu tạo gồm một ion dương +e và hai ion âm giống nhau nằm cân bằng. Khoảng cách giữa hai ion âm là α. Bỏ qua trọng lượng của các ion.
a) Hãy cho biết cấu trúc của hệ và khoảng cách giữa ion dương và ion âm (theo a).
b) Tính điện tích của một ion âm (theo e)
a) Trong trạng thái cân bằng, những lực điện tác dụng lên mỗi ion cân bằng lẫn nhau. Điều đó có nghĩa là tất cả các lực phải có cùng một giá hay ba ion phải nằm trên cùng một đường thẳng. Mặt khác, hai ion âm phải nằm đối xứng với nhau ở hai bên ion dương (Hình 1.2 G), thì lực điện do chúng tác dụng lên ion dương mới có thể cân bằng nhau.
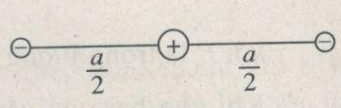
b) Xét sự cân bằng của một ion âm. Cường độ của lực đẩy giữa hai ion âm : \({F_d} = k{{{q^2}} \over {{a^2}}}\) , của lực hút giữa ion dương và ion âm : \({F_h} = k{{4\left| q \right|e} \over {{a^2}}}\)
Vì Fđ = Fh, nên |q| = 4e. Kết quả là q = – 4e.
Bài 1.9: Một hệ gồm ba điện tích dương q giống nhau và một điện tích Q nằm cân bằng. Ba điện tích q nằm tại ba đỉnh của một tam giác đều. Xác định dấu, độ lớn (theo q) và vị trí của điện tích Q.
Xét sự cân bằng của điện tích q nằm tại đỉnh C chẳng hạn của tam giác đều ABC cạnh a. Lực đẩy của mỗi điện tích q nằm ở A hoặc B tác dụng lên điện tích ở C :
Advertisements (Quảng cáo)
\(F = k{{{q^2}} \over {{a^2}}}\)
Hợp lực của hai lực đẩy có phương nằm trên đường phân giác của góc C, chiều hướng ra, cường độ:
\({F_d} = F\sqrt 3 = k{{{q^2}} \over {{a^2}}}\sqrt 3 \)
Muốn điện tích tại c nằm cân bằng thì phải có một lực hút cân bằng với lực đẩy (Hình 1.3G). Như vậy điện tích Q phải trái dấu với q (Q phải là điện tích âm) và phải nằm trên đường phân giác của góc C. Tương tự, Q cũng phải nằm trên các đường phân giác của các góc A và B. Do đó, Q phải nằm tại trọng tâm của tam giác ABC.
Khoảng cách từ Q đến C sẽ là:
\({F_d} = F\sqrt 3 = k{{{q^2}} \over {{a^2}}}\sqrt 3 \)
Cường độ của lực hút là:
\({F_h} = k{{3q|Q|} \over {{a^2}}}\). Với
\(F_d^{} = {F_h} \Rightarrow |Q| = {{\sqrt 3 } \over 3}q = 0,577q\)
Vậy Q = – 0,577q.
Bài 1.10: Hai quả cầu kim loại nhỏ, giống hệt nhau, chứa các điện tích cùng dấu q1 và q2, được treo vào chung một điểm O bằng hai sợi dây chỉ mảnh, không dãn, dài bằng nhau. Hai quả cầu đẩy nhau và góc giữa hai dây treo là 60°. Cho hai quả cầu tiếp xúc với nhau, rồi thả ra thì chúng đẩy nhau mạnh hơn và góc giữa hai dây treo bây giờ là 900. Tính tỉ số \({{{q_1}} \over {{q_2}}}\).
Gọi l là chiều dài của dây treo. Khi chưa trao đổi điện tích với nhau thì khoảng cách giữa hai quả cầu là l. Lực đẩy giữa hai quả cầu là :
\({F_1} = k{{{q_1}{q_2}} \over {{\ell ^2}}}\)
Tương tư như ở Hình 1.1 G, ta có : tan300= \({{{F_1}} \over P} = k{{{q_1}{q_2}} \over {P{\ell ^2}}}\) (1) với P là trọng lượng quả cầu.
Khi cho hai quả cầu trao đổi điện tích với nhau thì mỗi quả cầu mang điện tích
\({{{q_1} + {q_2}} \over 2}\) . Chúng vẫn đẩy nhau và khoảng cách giữa chúng bây
giờ là \(\ell \sqrt 2 \)
Lực đẩy giữa chúng bây giờ là :
\({F_2} = k{{{{({q_1} + {q_2})}^2}} \over {8{\ell ^2}}}\)
Tương tự như trên, ta có:
\(\tan {45^0} = {{{F_2}} \over P} = k{{{{({q_1} + {q_2})}^2}} \over {8P{\ell ^2}}}\) (2)
Từ (1) và (2) suy ra:
\(8\sqrt 3 {q_1}{q_2} = {({q_1} + {q_2})^2}\)
Chia hai vế cho q22ta có:
\(8\sqrt 3 {{{q_1}} \over {{q_2}}} = {\left( {{{{q_1}} \over {{q_2}}} + 1} \right)^2}\)
Đặt \({{{q_1}} \over {{q_2}}} = x\) ta có phương trình:
\(\eqalign{
& {x^2} + (2 – 8\sqrt 3 )x + 1 = 0 \cr
& \Leftrightarrow {x^2} – 11,86x + 1 = 0 \cr} \)
Các nghiệm của phương trình này là x1 = 11,77 và x2 = 0,085
