Bài 2.7: Cho tứ diện SABC. Trên SA, SB và SC lần lượt lấy các điểm D, E và F sao cho DE cắt AB tại I, EF cắt BC tại J, FD cắt CA tại K.
Chứng minh ba điểm I, J, K thẳng hàng.
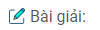
(h.2.26)
Ta có:
\(\eqalign{
& I = DE \cap AB \cr
& DE \subset \left( {DEF} \right) \Rightarrow I \in \left( {DEF} \right) \cr
& AB \subset \left( {ABC} \right) \Rightarrow I \in \left( {ABC} \right) \cr} \)
Lí luận tương tự thì J, K cũng lần lượt thuộc về hai mặt phẳng trên nên I, J, K thuộc về giao tuyến của (ABC) và (DEF) nên I, J, K thẳng hàng.
Bài 2.8: Cho hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) cắt nhau theo giao tuyến d. Trong \(\left( \alpha \right)\) lấy hai điểm A và B sao cho AB cắt d tại I. O là một điểm nằm ngoài \(\left( \alpha \right)\) và \(\left( \beta \right)\) sao cho OA và OB lần lượt cắt \(\left( \beta \right)\) tại A’ và B’.
a) Chứng minh ba điểm I, A’, B’ thẳng hàng.
b) Trong \(\left( \alpha \right)\) lấy điểm C sao cho A, B, C không thẳng hàng. Giả sử OC cắt \(\left( \beta \right)\) tại C’, BC cắt B’C’ tại J, CA cắt C’A’ tại K. Chứng minh I, J, K thẳng hàng.
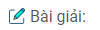
Advertisements (Quảng cáo)
(h.2.27)
a) I, A’, B’ là ba điểm chung của hai mặt phẳng (OAB) và \(\left( \beta \right)\) nên chúng thẳng hàng.
b) I, J, K là ba điểm chung của hai mặt phẳng (ABC) và (A’B’C’) nên chúng thẳng hàng.
Bài 2.9: Cho tứ diện S.ABC có D, E lần lượt trung điểm AC, BC và G là trọng tâm tam giác ABC. Mặt phẳng \(\left( \alpha \right)\) qua AC cắt SE, SB lần lượt tại M, N. Một mặt phẳng \(\left( \beta \right)\) qua BC cắt SD và SA lần lượt tại P và Q.
a) Gọi \(I = AM \cap DN,J = BP \cap EQ\). Chứng minh bốn điểm S, I, J, G thẳng hàng.
b) Giả sử \(AN \cap DM = K,BQ \cap EP = L\). Chứng minh ba điểm S, K, L thẳng hàng.
Advertisements (Quảng cáo)
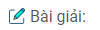
a) Ta thấy:
+ G là trọng tâm tam giác ABC \( \Rightarrow G \in BD\)
+ \(I \in DN\) (theo cách dựng hình).
+ \(J \in BP\) (theo cách dựng hình).
\( \Rightarrow S,I,J,G \in mp(SPN)\)
Tương tự \( \Rightarrow S,I,J,G \in mp(SQM)\)
Vậy \(S,I,J,G\) là điểm chung của \(mp(SPN)\) và \(mp(SQM)\)
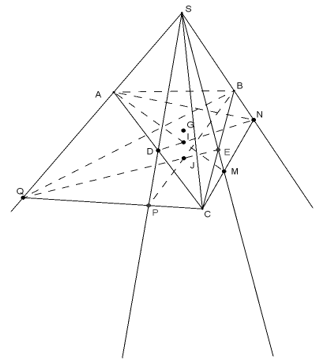
b)
Ta thấy:
+ \(S = PD \cap EM\)
+ \(K \in DM\)
+ \(L \in PE\)
\( \Rightarrow S,K,L \in (SPM)\)
Tương tự \( \Rightarrow S,K,L \in (SQN)\)
Vậy \(S,K,L\) là điểm chung của \((SPM)\) và \((SQN)\)

