Câu 148: Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy các điểm H, G sao cho BH = HG = GC. Qua H và G kẻ các đường vuông góc với BC, chúng cắt AB và AC theo thứ tự ở E và F. Tứ giác EFGH là hình gì ? Vì sao ?
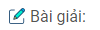
∆ ABC vuông cân tại A. \( \Rightarrow \widehat B = \widehat C = {45^0}\)
∆ BHE vuông tại H có \(\widehat B = {45^0}\)
⇒ ∆ BHE vuông cân tại H nên HB = HE
∆ CGF vuông cân tại G có \(\widehat C = {45^0}\)
⇒ ∆ CGF vuông cân tại G nên GC = GF
Ta có: BH = HG = GC (gt)
Suy ra: HE = HG = GF
EH // GF (hai đường thẳng cùng vuông góc với đường thẳng thứ ba)
nên tứ giác HEFG là hình bình hành (vì có một cặp cạnh đối song song bằng nhau)
có \(\widehat {EHG} = {90^0}\) do đó HEFG là hình chữ nhật
EH = HG (chứng minh trên)
Vậy HEFG là hình vuông.
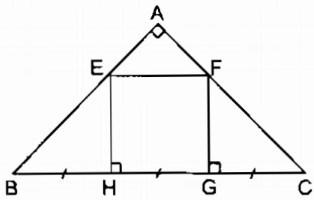
Câu 149: Cho hình vuông ABCD. Trên cạnh AD lấy điểm F, trên cạnh DC lấy điểm E sao cho AF = DE. Chứng minh rằng AE = BF và AE ⊥ BF.
Advertisements (Quảng cáo)
Xét ∆ ABF và ∆ DAE:
AB = DA (gt)
\(\widehat {BAF} = \widehat {ADE} = {90^0}\)
AF = DE (gt)
Do đó: ∆ ABF = ∆ DAE (c.g.c)
⇒ BF = AE
\({\widehat B_1} = {\widehat A_1}\)
Gọi H là giao điểm của AE và BF.
\(\widehat {BAF} = {\widehat A_1} + {\widehat A_2} = {90^0}\)
Suy ra: \({\widehat B_1} + {\widehat A_2} = {90^0}\)
Advertisements (Quảng cáo)
Trong ∆ ABH ta có:
\(\widehat {AHB} + {\widehat B_1} + {\widehat A_2} = {180^0}\)
\(\widehat {AHB} = {180^0} – \left( {{{\widehat B}_1} + {{\widehat A}_2}} \right) = {180^0} – {90^0} = {90^0}\)
Vậy AE ⊥ BF.
Câu 150: Cho một hình chữ nhật có hai cạnh kề không bằng nhau. Chứng minh rằng các tia phân giác của các góc hình chữ nhật đó cắt nhau tạo thành một hình vuông.
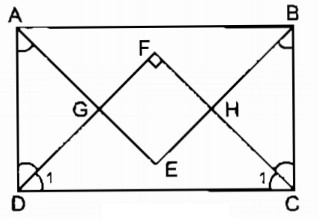
Gọi giao điểm các đường phân giác của các góc: \(widehat A,\widehat B,\widehat C,\widehat D\)theo thứ tự cắt nhau tại E, H, F, G.
Trong ∆ ADG ta có: \(\widehat {GAD} = {45^0};\widehat {GDA} = {45^0}\) (gt)
⇒ ∆ GAD vuông cân tại G
\( \Rightarrow \widehat {AGD} = {90^0}\)và GD = GA
\( \Rightarrow \widehat {FGE} = \widehat {AGD} = {90^0}\)
Trong ∆ BHC ta có:
\(\widehat {HBC} = {45^0};\widehat {HCB} = {45^0}\) (gt)
⇒ ∆HBC vuông cân tại H
\( \Rightarrow \widehat {BHC} = {90^0}\) và HB = HC
Trong ∆ FDC ta có: \({\widehat D_1} = {45^0};{\widehat C_1} = {45^0}\) (gt)
⇒ ∆ FDC vuông cân tại F \( \Rightarrow \widehat F = {90^0}\) và FD = FC
nên tứ giác EHFG là hình chữ nhật (vì có ba góc vuông)
Xét ∆ GAD và ∆ HBC :
\(\widehat {GAD} = \widehat {HBC} = {45^0}\)
AD = BC (tính chất hình chữ nhật)
\(\widehat {GDA} = \widehat {HCB} = {45^0}\)
Do đó: ∆ GAD = ∆ HBC (g.c.g) ⇒ GD = HC
FD = FC (chứng minh trên)
Suy ra: FG = FH
Vậy hình vuông EHFG có hai cạnh kề bằng nhau nên là hình vuông.

