Câu 144: Cho tam giác ABC vuông tại A, đường phân giác AD. Gọi M, N theo thứ tự là chân các đường vuông góc kẻ từ D đến AB, AC. Chứng minh rằng tứ giác AMDN là hình vuông.
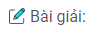
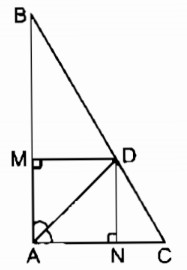
Xét tứ giác AMDN:
\(\widehat {MAN} = \)1v (gt)
DM ⊥ AB (gt)
\( \Rightarrow \widehat {AMD}\)= 1v
DN ⊥ AC (gt)
\( \Rightarrow \widehat {AND}\)=1v
Suy ra: Tứ giác AMDN là hình chữ nhật (vì có ba góc vuông), có đường chéo AD là đường phân giác của góc A.
Vậy : Hình chữ nhật AMDN là hình vuông.
Câu 145: Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lấy theo thứ tự các điểm E, K, P, Q sao cho AE = BK = CP = DQ. Tứ giác EKPQ là hình gì ? Vì sao ?
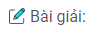
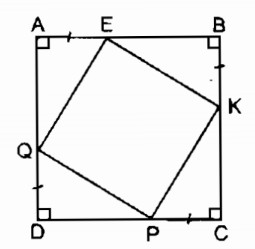
AB = BC = CD = DA (gt)
AE = BK = CP = DQ (gt)
Suy ra: EB = KC = PD = QA
– Xét ∆ AEQ và ∆ BKE :
AE = BK (gt)
\(\widehat A = \widehat B = {90^0}\)
QA = EB (chứng minh trên)
Do đó: ∆ AEQ = ∆ BKE (c.g.c) ⇒ EK = EQ (1)
– Xét ∆ BKE và ∆ CPK :
BK = CP (gt)
\(\widehat B = \widehat C = {90^0}\)
EB = KC (chứng minh trên)
Advertisements (Quảng cáo)
Do đó: ∆ BKE = ∆ CPK (c.g.c) ⇒ EK = KP (2)
Xét ∆ CPK và ∆ DQP :
CP = DQ (gt)
\(\widehat C = \widehat D = {90^0}\)
DP = CK (chứng minh trên)
Do đó: ∆ CPK = ∆ DQP (c.g.c) ⇒ KP = PQ (3)
Từ (1), (2) và (3) suy ra: EK = KP = PQ = EQ
Tứ giác EKPQ là hình thoi.
Câu 146: Cho tam giác ABC, điểm I nằm giữa B và C.
Qua I vẽ đường thẳng song song với AB, cắt AC ở H.
Qua I vẽ đường thẳng song song với AC, cắt AB ở K.
a. Tứ giác AHIK là hình gì ?
b. Điểm I nằm ở vị trí nào trên cạnh BC thì tứ giác AHIK là hình thoi ?
c. Tam giác ABC có điều kiện gì thì tứ giác AHIK là hình chữ nhật ?
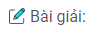
Advertisements (Quảng cáo)
a. Ta có: IK // AC (gt)
hay IK // AH
IH // AB (gt)
hay IH // AK
Vậy tứ giác AHIK là hình bình hành (theo định nghĩa)
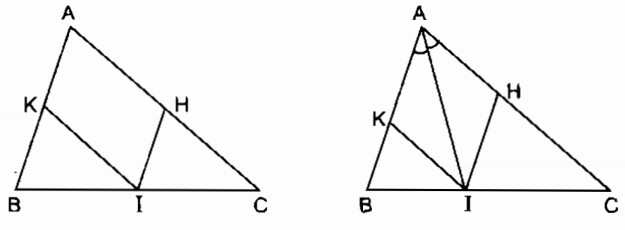
b. Hình bình hành AHIK là hình thoi nên đường chéo AI là phân giác của
Ngược lại AI là phân giác của . Hình bình hành AHIK có đường chéo là phân giác của một góc nên hình bình hành AHIK là hình thoi.
Vậy nếu I là giao điểm của đường phân giác của với cạnh BC thì tứ giác AHIK là hình thoi.
c. Hình bình hành AHIK là hình chữ nhật
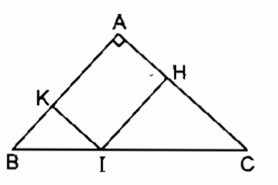
\( \Rightarrow \widehat A = {90^0}\)suy ra ∆ ABC vuông tại A
Ngược lại ∆ ABC có \(\widehat A = {90^0}\)
Suy ra: Hình bình hành AHIK là hình chữ nhật.
Vậy nếu ∆ ABC vuông tại A thì tứ giác AHIK là hình chữ nhật.
Câu 147: Hình chữ nhật ABCD có AB = 2AD. Gọi P, Q theo thứ tự là trung điểm của AB, CD. Gọi H là giao điểm của AQ và DP, gọi K là giao điểm của CP và BQ. Chứng minh rằng PHQK là hình vuông.
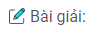
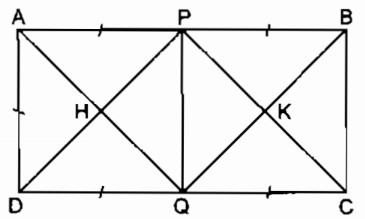
Xét tứ giác APQD ta có:
AB // CD (gt) hay AP // QD
AP = \({1 \over 2}\)AB (gt)
QD = \({1 \over 2}\)CD (gt)
Suy ra: AP = QD nên tứ giác APQD là hình bình hành.
\(\widehat A = {90^0}\)
Suy ra: Tứ giác APQD là hình chữ nhật
AD = AP = \({1 \over 2}\)AB
Vậy : Tứ giác APQD là hình vuông
⇒ AQ ⊥ PD (tính chất hình vuông) \( \Rightarrow \widehat {PHQ} = {90^0}\) (1)
HP = HQ (tính chất hình vuông)
– Xét tứ giác PBCQ ta có:
PB // CD
PB = \({1 \over 2}\)AB (gt)
CQ = \({1 \over 2}\)CD (gt)
Suy ra: PB = CQ nên tứ giác PBCQ là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
\(\widehat B = {90^0}\)suy ra tứ giác PBCQ là hình chữ nhật
PB = BC (vì cùng bằng AD = \({1 \over 2}\)AB)
Vậy: Tứ giác PBCQ là hình vuông
⇒ PC ⊥ BQ (tính chất hình vuông) \( \Rightarrow \widehat {PKQ} = {90^0}\)(2)
PD là tia phân giác \(\widehat {APQ}\) (tính chất hình vuông)
PC là tia phân giác \(\widehat {QPB}\) (tính chất hình vuông)
Suy ra: PD ⊥ PC (tính chất hai góc kề bù) ⇒ \(\widehat {HPK} = {90^0}\) (3)
Từ (1), (2) và (3) suy ra tứ giác PHQK là hình vuông.

