Câu 118: Tứ giác ABCD có AB ⊥ CD. Gọi E, F, G, H theo thứ tự là trung điểm của BC, BD, AD, AC. Chứng minh rằng EG = FH.
Trong ∆ BCD ta có:
E là trung điểm của BC (gt)
F là trung điểm của BD (gt)
nên EF là đường trung bình của ∆ BCD
⇒ EF // CD và EF= \({1 \over 2}\)CD (1)
Trong ∆ ACD ta có:
H là trung điểm của AC (gt)
G là trung điểm của AD (gt)
nên HG là đường trung bình của ∆ ACD
⇒ HG // AC và HG = \({1 \over 2}\)AC (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Mặt khác: EF // CD (chứng minh trên)
AB ⊥ CD(gt)
Suy ra EF ⊥ AB
Advertisements (Quảng cáo)
Trong ∆ ABC ta có HE là đường trung bình ⇒ HE // AB
Suy ra: HE ⊥ EF hay \(\widehat {FEH} = {90^0}\)
Vậy hình bình hành EFGH là hình chữ nhật.
Câu 119: Cho tam giác ABC, đường cao AH. Gọi D, E, M theo thứ tự là trung điểm của AB, AC, BC. Chứng minh rằng tứ giác DEMH là hình thang cân.
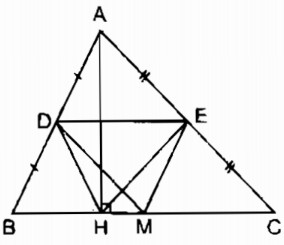
Vì D là trung điểm của AB (gt)
E là trung điểm của AC (gt)
nên DE là đường trung bình của tam giác ABC
⇒ DE // BC hay DE = HM
Advertisements (Quảng cáo)
Suy ra: Tứ giác DEMH là hình thang
M là trung điểm của BC (gt)
nên DM là đường trung bình của ∆ BAC
⇒ DM = \({1 \over 2}\)AC (tính chất đường trung bình của tam giác) (1)
Trong tam giác vuông AHC có\(\widehat {AHC} = {90^0}\).
HE là đường trung tuyến thuộc cạnh huyền AC.
⇒ HE = \({1 \over 2}\)AC (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: DM = HE
Vậy hình thang DEMH là hình thang cân (vì có hai đường chéo bằng nhau)
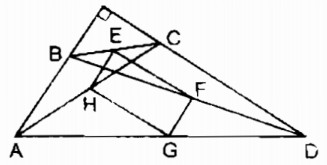
Câu 120: Cho tam giác ABC vuông tại A, điểm D thuộc cạnh AC. Gọi E, F, G theo thứ tự là trung điểm của BD, BC, DC. Chứng minh rằng tứ giác AEFG là hình thang cân.
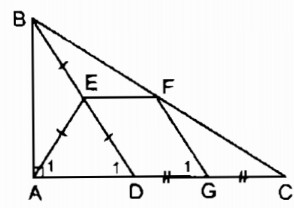
Trong ∆ BDC ta có:
E là trung điểm của BD (gt)
F là trung điểm của BC (gt)
nên EF là đường trung bình của ∆ BDC
⇒ EF // DC
hay EF // AG
Suy ra: Tứ giác AEFG là hình thang
G là trung điểm của DC (gt)
nên FG là đường trung bình của ∆ CBD
⇒ FG // BD ⇒ \({\widehat G_1} = {\widehat D_1}\) (đồng vị) (1)
Trong tam giác ABD vuông tại A có AE là trung tuyến thuộc cạnh huyền BD
⇒ AE = ED = \({1 \over 2}\)BD (tính chất tam giác vuông)
nên ∆ AED cân tại E \( \Rightarrow {\widehat A_1} = {\widehat D_1}\) (2)
Từ (1) và (2) suy ra: \({\widehat A_1} = {\widehat G_1}\)
Vậy hình thang AEFG là hình thang cân (theo định nghĩa).

