Câu 110: Chứng minh rằng các tia phân giác các góc của một hình bình hành cắt nhau tao thành một hình chữ nhật.
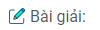
Gọi G, H, E, K lần lượt là giao điểm của các đường phân giác của \(\widehat A\) và\(\widehat B\); \(\widehat B\) và\(\widehat C\); \(\widehat C\) và\(\widehat D\); \(\widehat D\) và\(\widehat A\).
Ta có: \(\widehat {ADF} = {1 \over 2}\widehat {ADC}\) (gt)
\(\widehat {DAF} = {1 \over 2}\widehat {DAB}\) (gt)
\(\widehat {ADC} + \widehat {DAB} = {180^0}\) (hai góc trong cùng phía)
Suy ra: \(\widehat {ADF} + \widehat {DAF} = {1 \over 2}\left( {\widehat {ADC} + \widehat {DAB}} \right) = {1 \over 2}{.180^0} = {90^0}\)
Trong ∆ AFD ta có:
\(\widehat {AFD} = {180^0} – \left( {\widehat {ADF} + \widehat {DAF}} \right) = {180^0} – {90^0} = {90^0}\)
\(\widehat {EFG} = \widehat {AFD}\) (đối đỉnh)
\(\eqalign{ & \Rightarrow \widehat {EFG} = {90^0} \cr & \widehat {GAB} = {1 \over 2}\widehat {DAB}(gt) \cr & \widehat {GBA} = {1 \over 2}\widehat {CBA}(gt) \cr} \)
\(\widehat {DAB} + \widehat {CBA} = {180^0}\) (hai góc trong cùng phía)
\( \Rightarrow \widehat {GBA} + \widehat {GAB} = {1 \over 2}\left( {\widehat {DAB} + \widehat {CBA}} \right) = {1 \over 2}{.180^0} = {90^0}\)
Trong ∆ AGB ta có: \(\widehat {AGB} = {180^0} – \left( {\widehat {GAB} + \widehat {GBA}} \right) = {180^0} – {90^0} = {90^0}\)
hay \(\widehat G = {90^0}\)
\(\eqalign{ & \widehat {EDC} = {1 \over 2}\widehat {ADC}(gt) \cr & \widehat {ECD} = {1 \over 2}\widehat {BCD}(gt) \cr} \)
\(\widehat {ADC} + \widehat {BCD} = {180^0}\) (hai góc trong cùng phía)
\( \Rightarrow \widehat {EDC} + \widehat {ECD} = {1 \over 2}\left( {\widehat {ADC} + \widehat {BCD}} \right) = {1 \over 2}{.180^0} = {90^0}\)
Trong ∆ EDC ta có: \(\widehat {DEC} = {180^0} – \left( {\widehat {EDC} + \widehat {ECD}} \right) = {180^0} – {90^0} = {90^0}\)hay \(\widehat E = {90^0}\)
Advertisements (Quảng cáo)
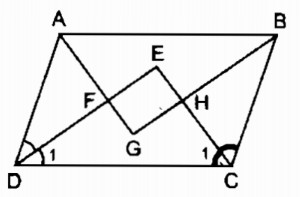
Câu 111: Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm các cạnh AB, BC, CD, DA . Tứ giác EFGH là hình gì ? Vì sao ?
Trong ∆ ABC ta có:
E là trung điểm của AB (gt)
F là trung điểm của BC (gt)
nên EF là đường trung bình của ∆ ABC
⇒ EF // AC và EF \( = {1 \over 2}\)AC (tính chất đường trung bình của tam giác) (1)
Trong ∆ DAC ta có:
H là trung điểm của AD (gt)
G là trung điểm của DC (gt)
nên HG là đường trung bình của ∆ DAC.
⇒ HG // AC và HG \( = {1 \over 2}\)AC (tính chất đường trung bình của tam giác) (2)
Advertisements (Quảng cáo)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Suy ra: Tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Ta lại có: BD ⊥ AC (gt)
EF // AC ( chứng minh trên)
Suy ra: EF ⊥ BD
Trong ∆ ABD ta có EH là đường trung bình ⇒ EH // BD
Suy ra: EF ⊥ EH hay \(\widehat {FEH} = {90^0}\)
Vậy hình bình hành EFGH là hình chữ nhật.
Câu 112: Tìm các hình chữ nhật trên hình 17 (trong hình 17b, O là tâm của đường tròn)
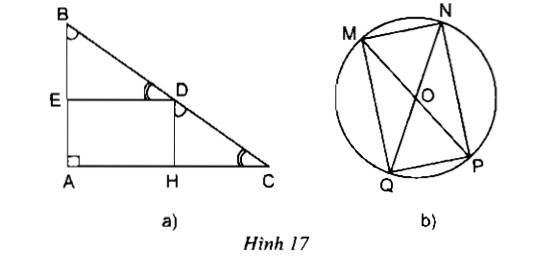
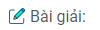
– Hình a ta có: \(\widehat B = \widehat {HDC}\)
⇒ AB // DH(vì có cặp góc đồng vị bằng nhau)
hay DH // AE
\(\widehat C = \widehat {BDE}\)
⇒ DE // AC (vì có cặp góc đồng vị bằng nhau)
hay DE // AH
\(\widehat A = {90^0}\)
Vậy : Tứ giác AHDE là hình chữ nhật.
– Hình b: Tứ giác MNPQ có:
OM = ON = OP = OQ
⇒ Tứ giác MNPQ có 2 đường chéo cắt nhau tại trung điểm của mỗi đường và bằng nhau. Vậy MNPQ là hình chữ nhật.
Câu 113: Các câu sau đúng hay sai ?
a. Hình chữ nhật là tứ giác có tất cả các góc bằng nhau.
b. Tứ giác có hai đường chéo bằng nhau là hình chữ nhật.
c. Tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường là hình chữ nhật.
a. Đúng vì hình chữ nhật có 4 góc vuông
b. Sai vì hình thang cân có hai cạnh bên không song song có hai đường chéo bằng nhau
c. Đúng vì hình chữ nhật có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

