Câu 78: Cho đường tròn (O ; 2cm) và (O’ ; 3cm), OO’ = 6cm.
a) Hai đường tròn (O), (O’) có vị trí tương đối như thế nào đối với nhau?
b) Vẽ đường tròn (O’ ; 1cm) rồi kẻ tiếp tuyến OA với đường tròn đó ( A là tiếp điểm). Tia O’A cắt đường tròn (O’ ; 3cm) ở B. Kẻ bán kính OC của đường tròn (O) song song với O’B, B và C thuộc cùng một nửa mặt phẳng có bờ OO’. Chứng minh rằng BC là tiếp tuyến chung của hai đường tròn (O ; 2cm) và (O’ ; 3cm).
c) Tính độ dài BC.
d) Gọi I là giao điểm của BC và OO’. Tính độ dài IO.
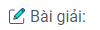
a) Vì OO’ = 6 > 2 + 3 hay OO’ > R + R’ nên hai đường tròn (O) và (O’) ở ngoài nhau.
b) Xét tứ giác ABCO ta có:
AB // CO (gt) (1)
Mà: AB = O’B – O’A = 3 – 1 = 2 (cm)
Suy ra: AB = OC = 2 (cm) (2)
Từ (1) và (2) suy ra: ABCO là hình bình hành.
Lại có: OA ⊥ O’A ( tính chất tiếp tuyến)
Suy ra: \(\widehat {OAO’} = 90^\circ \) hay \(\widehat {OAB} = 90^\circ \)
Tứ giác ABCO là hình chữ nhật
Suy ra: \(\widehat {OCB} = \widehat {ABC} = 90^\circ \)
Suy ra: BC ⊥ OC và BC ⊥ O’B
Vậy BC là tiếp tuyến chung của hai đường tròn (O) và (O’).
Advertisements (Quảng cáo)
c) Vì tứ giác ABCO là hình chữ nhật nên OA = BC
Áp dụng định lí Pi-ta-go vào tam giác vuông OAO’, ta có:
OO’2 = OA2 + O’A2
⇒OA2 = OO’2 – O’A2 = 62 – 12 = 35
\(⇒ OA =\sqrt {35}(cm)\)
Vậy \(BC = \sqrt {35} (cm)\)
d) Trong tam giác O’BI có OC // O’B
Suy ra: \({{IO} \over {IO’}} = {{OC} \over {O’B}}\) (hệ quả định lí Ta-lét)
\(⇒{{IO} \over {IO’ – IO}} = {{OC} \over {O’B – OC}} \Rightarrow {{IO} \over {O’O}} = {2 \over {3 – 2}} \Rightarrow {{IO} \over 6} = {2 \over 1}\)
Vậy \(OI = {{6.2} \over 1} = 12 (cm)\)
Câu 79: Cho đường tròn (O ; R), điểm A nằm bên ngoài đường tròn (R < OA < 3R). Vẽ đường tròn (A ; 2R).
a) Hai đường tròn (O) và (A) có vị trí tương đối như thế nào đối với nhau?
Advertisements (Quảng cáo)
b) Gọi B là một giao điểm của hai đường tròn trên. Vẽ đường kính BOC của đường tròn (O). Gọi D là giao điểm ( khác C) của AC và đường tròn (O). Chứng minh rằng AD = DC.
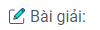
a) Ta có: R < OA < 3R ⇔ 2R- R < OA < 2R + R
Suy ra hai đường tròn (O; R) và (A; 2R) cắt nhau.
b) Tam giác BCD nội tiếp trong đường tròn (O) có BC là đường kính nên \(\widehat {BDC} = 90^\circ \)
Suy ra: BD ⊥ AC (1)
Ta có: AB = 2R và BC = 2OB = 2R
Suy ra tam giác ABC cân tại B (2)
Từ (1) và (2) suy ra: AD = DC
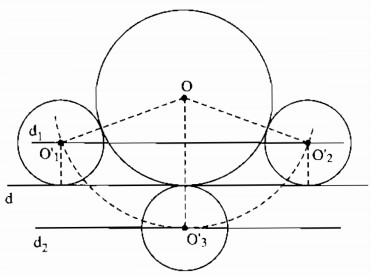
Câu 80: Cho đường tròn (O ; 2cm) tiếp xúc với đường thẳng d. Dựng đường tròn (O’ ; 1cm) tiếp xúc với đường thẳng d và tiếp xúc ngoài đường tròn (O).
* Phân tích
− Giả sử dựng được đường tròn (O’; 1cm) tiếp xúc với đường thẳng d và tiếp xúc ngoài với đường tròn (O ; 2cm).
− Đường tròn (O; 1cm) tiếp xúc với d nên O’ cách d một khoảng bằng 1cm. Khi đó O’ nằm trên hai đường thẳng d1, d2 song song với d và cách d một khoảng 1cm.
− Đường tròn (O’; 1cm) tiếp xúc với đường tròn (O; 2cm) nên suy ra OO’ = 3cm. Khi đó O’ là giao điểm của (O; 3cm) với d1 và d2.
* Cách dựng
− Dựng hai đường tròn d1 và d2 song song với d và cách d một khoảng bằng 1cm.
− Dựng đường tròn (O; 3cm) cắt tại d1 tại O’1. Vẽ (O’1; 1cm) tiếp xúc với d.
* Chứng minh
Theo cách dựng, O’1 cách d một khoảng bằng 1cm nên (O’1; 1cm) tiếp xúc với d.
Vì OO’1 = 3cm nên (O’1; 1cm) tiếp xúc với (O; 2cm)
* Biện luận: O cách d1 một khoảng bằng 1cm nên (O; 3cm) cắt d1 tại hai điểm phân biệt.

