Câu 81: Cho đoạn thẳng AB, điểm C nằm giữa A và B. Vẽ về một phía của AB các nửa đường tròn có đường kính theo thứ tự là AB, AC, CB. Đường vuông góc với AB tại C cắt nửa đường tròn lớn tại D. DA, DB cắt các nửa đường tròn có đường kính AC, CB theo thứ tự M, N.
a) Tứ giác DMCN là hình gì ?Vì sao ?
b) Chứng minh hệ thức DM.DA = DN.DB.
c) Chứng minh rằng MN là tiếp tuyến chung của các nửa đường tròn có đường kính AC và CB.
d) Điểm C ở vị trí nào trên AB thì MN có độ dài lớn nhất ?
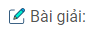
a) Tam giác ABD nội tiếp trong đường tròn có AB là đường kính nên \(\widehat {BDA} = 90^\circ \) hay \(\widehat {MDN} = 90^\circ \)
Tam giác ACM nội tiếp đường tròn có AC là đường kính nên \(\widehat {AMC} = 90^\circ \)
Suy ra: \(CM ⊥ AD ⇒\widehat {CMD} = 90^\circ \)
Tam giác BCN nội tiếp trong đường tròn có BC là đường kính nên \(\widehat {BNC} = 90^\circ \)
Suy ra: \(CN ⊥ BD ⇒ \widehat {CND} = 90^\circ \)
Tứ giác CMDN có ba góc vuông nên nó là hình chữ nhật.
b) Tam giác ACD vuông tại C có CM ⊥ AD.
Theo hệ thức lượng trong tam giác vuông, ta có:
\(C{D^2} = DM.DA\) (1)
Tam giác BCD vuông tại C nên CN ^ BD.
Theo hệ thức lượng trong tam giác vuông, ta có:
\(C{D^2} = DN.DB\) (2)
Từ (1) và (2) suy ra: DM.DA = DN.DB
c) Gọi P là trung điểm của AC, Q là trung điểm của BC, I là giao điểm của MN với DC.
Vì CMDN là hình chữ nhật nên IC = IM = ID = IN
Tam giác CNI cân tại I nên \(\widehat {ICN} = \widehat {INC}\) (3)
Tam giác CNQ cân tại Q nên \(\widehat {QCN} = \widehat {QNC}\) (4)
Vì AB ^ CD nên \(\widehat {ICN} + \widehat {QCN} = 90^\circ \) (5)
Từ (3), (4) và (5) suy ra: \(\widehat {INC} + \widehat {QNC} = 90^\circ \) hay MN ^ QN
Vậy MN là tiếp tuyến của đường tròn đường kính BC.
Tam giác CMI cân tại I nên \(\widehat {ICM} = \widehat {IMC}\) (6)
Tam giác CMP cân tại P nên \(\widehat {PCM} = \widehat {PMC}\) (7)
Vì AB ⊥ CD nên \(\widehat {PCM} + \widehat {ICM} = 90^\circ \) (8)
Từ (6), (7) và (8) suy ra: \(\widehat {PMC} + \widehat {IMC} = 90^\circ \) hay MN ⊥ PM
Vậy MN là tiếp tuyến của đường tròn đường kính AC.
d) Gọi O là trung điểm của AB
Tứ giác CMDN là hình chữ nhật nên CD = MN
Trong tam giác OCD ta có: \(CD \le OD\) nên \(MN \le OD\)
Vì OD không đổi nên MN = OD là giá trị lớn nhất khi và chỉ khi C trùng với O.
Vậy C là trung điểm của AB thì MN có độ dài lớn nhất.
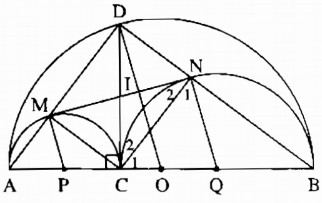
Câu 82: Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài DE, D ∈ (O), E ∈ (O’). Kẻ tiếp tuyến chung tại A, cắt DE ở I. Gọi M là giao điểm của OI và AD, N là giao điểm của O’I và AE.
Advertisements (Quảng cáo)
a) Tứ giác AMIN là hình gì ? Vì sao ?
b) Chứng minh hệ thức IM.IO = IN.IO’.
c) Chứng minh rằng OO’ là tiếp tuyến của đường tròn có đường kính là DE.
d) Tính độ dài DE biết rằng OA = 5cm, O’A = 3,2cm.
a) Trong đường tròn (O) ta có OI là tia phân giác
của góc AID ( tính chất hai tiếp tuyếnc cắt nhau)
Trong đường tròn (O’) ta có O’I là tia phân giác của góc AIE ((tính chất hai tiếp tuyến cắt nhau)
Þ IO ⊥ IO’ ( tính chất kề bù)
Suy ra: \(\widehat {OIO’} = 90^\circ \) hay \(\widehat {MIN} = 90^\circ \)
Lại có: IA = ID ((tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác ADI có IO là phân giác của góc AID nên IO cũng là đường cao của tam giác AID.
Suy ra: IO ⊥ AD hay \(\widehat {AMI} = 90^\circ \)
Mặt khác: IA = IE ((tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác AEI cân tại I.
Tam giác cân AIE có IO’ là phân giác của góc AIE nên IO¢ cũng là đường cao của tam giác AIE.
Suy ra: IO’ ⊥ AE hay \(\widehat {ANI} = 90^\circ \)
Tứ giác AMIN có ba góc vuông nên nó là hình chữ nhật.
b) Tam giác AIO vuông tại A có AM ⊥ IO.
Theo hệ thức lượng trong tam giác vuông, ta có:
IA2 = IM.IO (1)
Tam giác AIO’ vuông tại A có AN ⊥ IO’.
Theo hệ thức lượng trong tam giác vuông, ta có:
Advertisements (Quảng cáo)
IA2 = IN.IO’ (2)
Từ (1) và (2) suy ra: IM.IO = IN.IO’
c) Ta có: IA = ID = IE ( chứng minh trên)
Suy ra A nằm trên đường tròn tâm I đường kính DE.
Vì OO’ ⊥ IA tại A nên OO’ là tiếp tuyến của đường tròn \(\left( {I;{{DE} \over 2}} \right).\)
d) Tam giác O’IO vuông tại I có IA ⊥ OO’.
Theo hệ thức lượng trong tam giác vuông, ta có:
IA2 = OA.O’A = 5.3,2 = 16
Suy ra: IA = 4 (cm). Mà DE = 2IA nên DE = 2.4 = 8 (cm).
Câu 83*: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B, OO’ = 3cm. Qua A kẻ một đường thẳng cắt các đường tròn (O) và (O’) theo thứ tự tại E và F ( A nằm giữa E và F). Tính xem đoạn thẳng EF có độ dài lớn nhất bằng bao nhiêu?
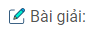
Kẻ OI ⊥ AE, O’K ⊥ AF
Trong đường tròn (O), ta có:
\( IA = IE = {1 \over 2}AE\) ( đường kính vuông góc với dây cung)
Trong đường tròn (O’), ta có:
\(KA = KF = {1 \over 2}AF\) (đường kính vuông góc với dây cung)
Ta có: EF = AE = AF
Suy ra: EF = 2IA = 2AK = 2(IA + AK) = 2IK (1)
Kẻ O’H ⊥ OI
Khi đó tứ giác IHO’K là hình chữ nhật ( có ba góc vuông)
Suy ra: O’H = IK
Trong tam giác OHO’ ta có: \(O’H \le {\rm{OO’}}\) =3 (cm)
Suy ra: \(IK \le {\rm{OO}}’\) (2)
Từ (1) và (2) suy ra: \(EF \le {\rm{2OO’}}= 6 (cm)\)
Ta có: EF = 6cm khi H và O trùng nhau hay EF // OO’
Vậy EF có độ dài lớn nhất bằng 6cm khi và chỉ khi EF // OO’.
Câu 84: Cho tam giác ABC vuông tại A ( AB < AC) nội tiếp đường tròn (O) có đường kính BC. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F. Chứng minh rằng:
a) Tam giác EBF là tam giác cân ;
b) Tam giác HAF là tam giác cân ;
c) HA là tiếp tuyến của đường tròn (O).
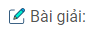
a) Gọi I là giao điểm của AD và BC
Vì BC là đường trung trực của AD nên theo tính chất đường trung trực ta có:
BA = BD
Tam giác BAD cân tại B có BI ⊥ AD nên BI là tia phân giác của góc ABD.
Suy ra: \(\widehat {ABI} = \widehat {DBI}\)
Mà \(\widehat {ABI} = \widehat {HBF}\) (đối đỉnh)
và \(\widehat {DBI} = \widehat {HBE}\) ( đối đỉnh)
Suy ra: \(\widehat {HBE} = \widehat {HBF}\)
Tam giác EBF có BH là tia phân giác của góc EBF và BH ⊥ EF nên tam giác EBF cân tại B.
b) Tam giác EBF cân tại B nên HE = HF
Tam giác AEF vuông tại A có AH là đường trung tuyến ứng với cạnh huyền nên:
\(HA = HE = HF = {1 \over 2}{\rm{EF}}\) (tính chất tam giác vuông)
Vậy tam giác AHF cân tại H.
c) Tam giác AHF cân tại H nên \(\widehat {HAF} = \widehat {HFA}\) (1)
Tam giác AOB cân tại O nên \(\widehat {OAB} = \widehat {OBA}\)
Mà \(\widehat {ABI} = \widehat {HBF}\) ( đối đỉnh)
Suy ra: \(\widehat {OAB} = \widehat {HBF}\) (2)
Từ (1) và (2) suy ra: \(\widehat {HAO} = \widehat {{\rm{HAF}}} + \widehat {OAB} = \widehat {HFB} + \widehat {HBF}\) (3)
Tam giác BHF vuông tại H nên \(\widehat {HFB} + \widehat {HBF} = 90^\circ \) (4)
Từ (3) và (4) suy ra: \(\widehat {HAO} = 90^\circ \) hay HA ⊥ AO
Vậy HA là tiếp tuyến của đường tròn (O).

