Câu 8.1: Cho hai đường tròn (O ; R) và (O’ ; r). Điền vào chỗ trống của bảng sau
|
R |
r |
OO’ |
Hệ thức giữa OO’, R, r |
Vị trí tương đối của (O) và (O’) |
|
3 |
1 |
… |
OO’ = R – r |
… |
|
3 |
1 |
… |
… |
Tiếp xúc ngoài |
|
3 |
1 |
3,5 |
… |
… |
|
3 |
1 |
5 |
… |
… |
|
3 |
1 |
1 |
… |
… |
|
R |
r |
OO’ |
Hệ thức giữa OO’, R, r |
Vị trí tương đối của (O) và (O’) |
|
3 |
1 |
2 |
\(OO’ = R – r\) |
Tiếp xúc trong |
|
3 |
1 |
4 |
\(OO’ = R + r\) |
Tiếp xúc ngoài |
|
3 |
1 |
3,5 |
\(R – r < OO'< R + r\) |
Cắt nhau |
|
3 |
1 |
5 |
\(OO’> R + r\) |
Ở ngoài nhau |
|
3 |
1 |
1 |
\(OO'< R – r\) |
(O) đựng (O’) |
Câu 8.2: Cho hai đường tròn (O ; 3cm) và (O ; 4cm) có OO’ = 5cm.
a) Hai đường tròn (O) và (O¢) có vị trí tương đối nào ?
b) Tính độ dài dây chung của hai đường tròn.
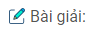
a) (O) và (O’) cắt nhau.
b) Gọi A và B là giao điểm của hai đường tròn (O)
Advertisements (Quảng cáo)
và (O’), H là giao điểm của AB và OO’.
Tam giác AOO’ vuông tại A, AH ⊥ OO’ và AB = 2AH.
Ta tính được AH = 2,4cm nên AB = 4,8cm.
Câu 8.3: Cho đường tròn (O) và điểm A cố định trên đường tròn. Điểm B chuyển động trên đường tròn
Advertisements (Quảng cáo)
a) Chứng minh rằng trung điểm M của AB chuyển động trên một đường tròn (O¢).
b) Đường tròn (O¢) có vị trí tương đối nào đó đối với đường tròn (O) ?
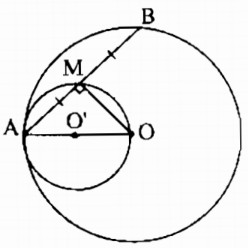
a) \(\widehat {AMO} = 90^\circ \). Điểm M chuyển động trên
đường tròn (O’) đường kính AO.
b) Đường tròn (O’) tiếp xúc trong với đường tròn (O).

