Câu 71: Cho I là trung điểm của đoạn thẳng AB. Vẽ các đường tròn (I ; IA) và (B ; BA)
a) Hai đường tròn (I) và (B) nói trên có vị trí tương đối như thế nào đối với nhau? Vì sao?
b) Kẻ một đường thẳng đi qua A, cắt các đường tròn (I) và (B) theo thứ tự tại M và N. So sánh các độ dài AM và MN.
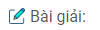
a) Vì A, I , B thẳng hàng nên:
BI = AB – AI
Vậy đường tròn (I ; IA) tiếp xúc với đường tròn (B; BA) tại A.
b) Tam giác AMB nội tiếp trong đường tròn (I) có AB là đường kính nên \(\widehat {AMB} = 90^\circ \)
Suy ra: AM ⊥ BM hay BM ⊥ AN
Suy ra: AM = AN ( đường kính vuông góc dây cung).
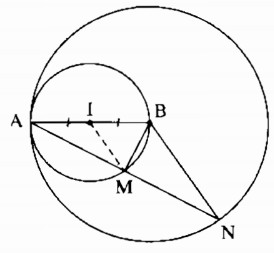
Câu 72: Cho hai đường tròn đồng tâm O. Gọi AB là dây bất kỳ của đường tròn nhỏ. Đường thẳng AB cắt đường tròn lớn ở C và D ( nằm giữa B và C). So sánh các độ dài AC và BD.
Kẻ OI ⊥ AB. Ta có: OI ⊥ CD
Trong đường tròn (O) (nhỏ) ta có: OI ⊥ AB
Suy ra:
IA = IB ( đường kính vuông góc dây cung) (1)
Advertisements (Quảng cáo)
Trong đường tròn (O) (lớn) ta có: OI ⊥ CD
Suy ra:
IC = ID ( đường kính vuông góc dây cung)
Hay IA + AC = IB + BD (2)
Từ (1) và (2) suy ra: AC = BD.
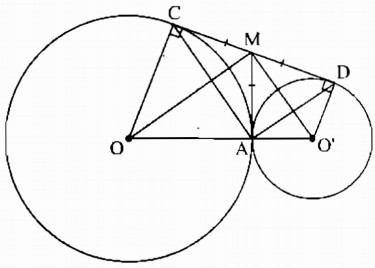
Câu 73: Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Gọi CD là tiếp tuyến chung ngoài của hai đường tròn ( C ∈ (O), D ∈ (O’)).
a) Tính số đo góc CAD.
b) Tính độ dài CD biết OA = 4,5cm, O’A = 2cm..
Advertisements (Quảng cáo)
a) Kẻ tiếp tuyến chung tại A cắt CD tại M
Trong đường tròn (O) ta có:
MA = MC (tính chất hai tiếp tuyến cắt nhau)
Trong đường tròn (O’) ta có:
MA = MD (tính chất hai tiếp tuyến cắt nhau)
Suy ra: \(MA = MC = MD = {1 \over 2}CD\)
Tam giác ACD có đường trung tuyến AM ứng với cạnh CD và bằng nửa cạnh CD nên tam giác ACD vuông tại A
Suy ra: \(\widehat {CAD} = 90^\circ \)
b) Ta có:
MO là tia phân giác của \(\widehat {CMA}\) (tính chất hai tiếp tuyến cắt nhau)
MO’ là tia phân giác của \(\widehat {DMA}\) (tính chất hai tiếp tuyến cắt nhau)
Suy ra: MO ⊥ MO’ (tính chất hai góc kề bù)
Tam giác MOO’ vuông tại M có MA ⊥ OO’ ( tính chất tiếp tuyến)
Theo hệ thức lượng trong tam giác vuông, ta có:
MA2 = OA.O’A = 4,5.2 = 9 ⇒ MA = 3 (cm)
Mà \(MA = {1 \over 2}CD ⇒ CD = 2.MA = 2.3 = 6 (cm)\)
Câu 74: Cho hai đường tròn đồng tâm O. Một đường tròn (O’) cắt một đường tròn tâm O tại A, B và cắt đường tròn tâm O còn lại tại C, D. Chứng minh rằng AB // CD.
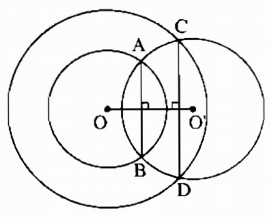
Vì đường tròn (O’) cắt đường tròn ( O; OA) tại A và B nên OO’ là trung trực của AB
Suy ra: OO’ ⊥ AB (1)
Vì đường tròn (O’) cắt đường tròn (O; OC) tại C và D nên OO’ là trung trực của CD
Suy ra: OO’ ⊥ CD (2)
Từ (1) và (2) suy ra: AB // CD.

