Câu 42: Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Dùng thước và compa, hãy dựng các điểm B và C thuộc đường tròn (O) sao cho AB và AC là các tiếp tuyến của đường tròn (O).
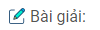
* Phân tích
Giả sử tiếp tuyến AB và AC cần dựng thỏa mãn điều kiện bài toán.
Ta có: AB ⊥ OB \(\widehat {ABO} = 90^\circ \)
\(AC \bot OC \Rightarrow \widehat {ACO} = 90^\circ \)
Tam giác ABO có \(\widehat {ABO} = 90^\circ \) nội tiếp trong đường tròn đường kính AO và tam giác ACO có \(\widehat {ACO} = 90^\circ \) nội tiếp trong đường tròn đường kính AO.
Suy ra B và C là giao điểm của đường tròn đường kính AO với đường tròn (O).
* Cách dựng
− Dựng I là trung điểm của OA.
− Dựng đường tròn ( I; IO) cắt đường tròn (O) tại B và C.
− Nối AB, AC ta được hai tiếp tuyến cần dựng.
* Chứng minh
Tam giác ABO nội tiếp trong đường tròn (I) có OA là đường kính nên: \(\widehat {ABO} = 90^\circ \)
Suy ra: AB ⊥ OB tại B nên AB là tiếp tuyến của đường tròn (O).
Tam giác ACO nội tiếp trong đường tròn (I) có OA là đường kính nên : \(\widehat {ACO} = 90^\circ \)
Advertisements (Quảng cáo)
Suy ra: AC ⊥ OC tại C nên AC là tiếp tuyến của đường tròn (O)
* Biện luận
Luôn dựng được đường tròn tâm I, cắt đường tròn tâm O tại hai điểm B và C và luôn có AB, AC là hai tiếp tuyến của đường tròn (O).
Câu 43: Cho điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d. Dựng đường tròn (O) đi qua A và B, nhận đường thẳng d làm tiếp tuyến.
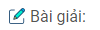
* Phân tích
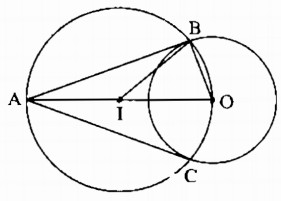
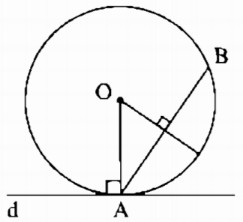
− Giả sử dựng được đường tròn (O) qua A, B và tiếp xúc với d. Khi đó đường tròn (O) phải tiếp xúc với d tại A.
− Đường tròn (O) đi qua A và B nên tâm O nằm trên đường trung trực của AB.
− Đường tròn (O) tiếp xúc với d tại A nên điểm O nằm trên đường thẳng vuông góc với d tại điểm A.
Advertisements (Quảng cáo)
* Cách dựng
− Dựng đường thẳng trung trực của AB.
− Dựng đường thẳng đi qua A và vuông góc với d. Đường thẳng này cắt đường trung trực của AB tại O.
− Dựa đường tròn ( O; OA) ta được đường tròn cần dựng.
* Chứng minh
Vì O nằm trên đường trung trực của AB nên OA = OB. Khi đó đường tròn (O; OA) đi qua hai điểm A và B.
Ta có: OA vuông góc với d tại A nên d là tiếp tuyến của (O).
Vậy (O) thỏa mãn điều kiện bài toán.
Câu 44: Cho tam giác ABC vuông tại A. Vẽ đường tròn (B ; BA) và đường tròn (C ; CA), chúng cắt nhau tại điểm D (khác A). Chứng minh rằng CD là tiếp tuyến của đường tròn (B).
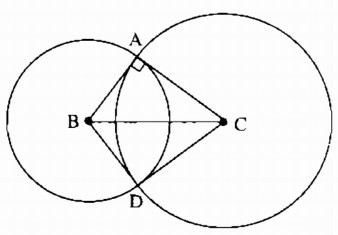
Xét hai tam giác ABC và DBC, ta có:
BA = BD (bán kính của (B; BA))
CA = CD (bán kính của (C; CA))
BC chung
Suy ra: ∆ABC = ∆DBC (c.c.c)
Suy ra: \(\widehat {BAC} = \widehat {BDC}\)
Mà \(\widehat {BAC} = 90^\circ \) (gt) \( \Rightarrow \widehat {BDC} = 90^\circ \)
Suy ra: CD ⊥ BD tại D
Vậy CD là tiếp tuyến của đường tròn (B; BA).

