Câu 41*: Cho nửa đường tròn tâm O, đường kính AB. Qua điểm C thuộc nửa đường tròn, kẻ tiếp tuyến d của đường tròn. Gọi E và F lần lượt là chân các đường vuông góc kẻ từ A đến B đến d. Gọi H là chân đường vuông góc kẻ từ C đến AB. Chứng minh rằng:
a) CE = CF;
b) AC là tia phân giác của góc BAE;
c) \(C{H^2} = AE.BF\).
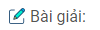
a) Ta có: OC ⊥d ( tính chất tiếp tuyến)
AE ⊥ d (gt)
BF ⊥ d (gt)
Suy ra: OC // AE // BF
Mà OA = OB (=R)
Suy ra: CE = CF (tính chất đường thẳng song cách đều)
b) Ta có: AE // OC
Suy ra: \(\widehat {OCA} = \widehat {EAC}\) ( hai góc sole trong) (1)
Ta có: OA = OC (=R)
Suy ra: ∆OAC cân tại O \( \Rightarrow \widehat {OCA} = \widehat {OAC}\) (2)
Từ (1) và (2) suy ra: \(\widehat {EAC} = \widehat {OAC}\)
Vậy AC là tia phân giác của góc OAE hay AC là tia phân giác của góc BAE.
c) Tam giác ABC nội tiếp trong đường tròn (O) có AB là đường kính nên \(\widehat {ACB} = 90^\circ \)
Tam giác ABC vuông tại C có CH ⊥ AB.
Advertisements (Quảng cáo)
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
\(C{H^2} = HA.HB\) (3)
Xét hai tam giác ACH và ACE, ta có:
\(\widehat {AEC} = \widehat {AHC} = 90^\circ \)
CH = CE (tính chất đường phân giác)
AC chung
Suy ra: ∆ACH = ∆ACE (cạnh huyền, cạnh góc vuông)
Suy ra: AH = AE (4)
Xét hai tam giác BCH và BEF, ta có:
\(\widehat {BHC} = \widehat {BFC} = 90^\circ \)
CH = CF (= CE)
BC chung
Advertisements (Quảng cáo)
Suy ra: ∆BCH = ∆BCF (cạnh huyền, cạnh góc vuông)
Suy ra: BH = BF (5)
Từ (3), (4) và (5) suy ra: \(C{H^2} = AE.BF\)
Câu 4.1: Cho đoạn thẳng AB. Đường tròn (O) đường kính 2cm tiếp xúc với đường thẳng AB. Tâm O nằm trên
(A) Đường vuông góc với AB tại A ;
(B) Đường vuông góc với AB tại B ;
(C) Hai đường thẳng song song với AB và cách AB một khoảng 1cm ;
(D) Hai đường thẳng song song với AB và cách AB một khoảng 2cm.
Hãy chọn phương án đúng.
Chọn (C).
Câu 4.2: Cho đường tròn (O ; 2cm), điểm A di chuyển trên đường tròn. Trên tiếp tuyến tại A, lấy điểm M sao cho AM = OA. Điểm M chuyển động trên đường nào ?
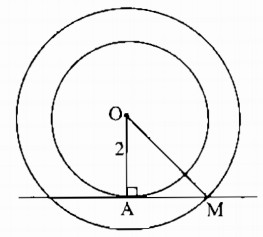
\(OM = 2\sqrt 2 \).
Điểm M chuyển động trên đường tròn \((O ; 2\sqrt 2 cm).\)
Câu 4.3: Cho đường tròn (O ; 15cm), dây AB = 24cm. Một tiếp tuyến song song với AB cắt các tia OA, OB theo thứ tự ở E, F. Tính độ dài EF.
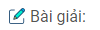
Gọi C là tiếp điểm của EF với đường
tròn (O), H là giao điểm của OC và AB. Ta có
OC ^ EF và AB // EF nên OC ^ AB.
Ta tính được HB = 12 cm nên OH = 9 cm.
∆OAB đồng dạng với ∆OEF nên \({{OH} \over {OC}} = {{AB} \over {EF}}\) ,
tức là \({9 \over {15}} = {{24} \over {EF}}\).
Ta tính được EF = 40 cm.

