Câu 10: Cho tam giác ABC có AB > AC. Trên cạnh AB lấy một điểm D sao cho hạ AD = AC.
Vẽ đường tròn tâm O ngoại tiếp tam giác DBC. Từ O lần lượt hạ các đường thẳng vuông góc OH, OK xuống BC và BD (\(H \in BC,K \in BD\)).
a) Chứng minh rằng OH < OK.
b) So sánh hai cung nhỏ BD và BC.
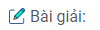
a) Trong ∆ABC ta có:
BC > AB – AC (bất đẳng thức tam giác)
Mà AC = AD (gt)
\( \Rightarrow \) BC > AB – AD
Hay BC > BD
Trong (O) ta có: BC > BD
\( \Rightarrow \) OH < OK (dây lớn hơn gần tâm hơn)
b) Ta có dây cung BC > BD
Suy ra: \(\overparen{BC}\) > \(\overparen{BD}\) (dây lớn hơn căng cung lớn hơn).
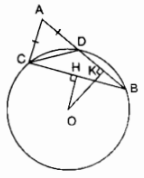
Câu 11: Trên dây cung AB của một đường tròn O, lấy hai điểm C và D chia dây này thành ba đoạn thẳng bằng nhau AC = CD = DB. Các bán kính qua C và D cắt cung nhỏ AB lần lượt tại E và F. Chứng minh rằng:
a) \(\overparen{AE}\) = \(\overparen{FB}\);
b) \(\overparen{AE}\) < \(\overparen{EF}\).
a) ∆OABcân tại O (vì OA = OB bán kính)
\( \Rightarrow \widehat A = \widehat B\)
Xét ∆OAC và ∆OBD:
OA = OB (bán kính)
Advertisements (Quảng cáo)
\(\widehat A = \widehat B\) (chứng minh trên)
AC = BD (gt)
Suy ra: ∆OAC = ∆OBD (c.g.c)
\( \Rightarrow \widehat {{O_1}} = \widehat {{O_2}}\) (1)
sđ \(\overparen{AE}\) \( = \widehat {{O_1}}\) (2)
sđ \(\overparen{BF}\) \( = \widehat {{O_2}}\) (3)
Từ (1), (2) và (3) suy ra: \(\overparen{AE}\) = \(\overparen{BF}\)
b) ∆OAC = ∆BOD (chứng minh trên)
\( \Rightarrow OC = OD\)
\( \Rightarrow \Delta OCD\) cân tại O nên \(\widehat {ODC} < {90^0}\). Suy ra: \(\widehat {CDF} > {90^0}\)
Trong ∆CDF ta có: \(\widehat {CDF} > {90^0} \Rightarrow CF > CD\) nên AC < CF
Xét ∆OAC và ∆OCF:
OA = OF (bán kính)
OC cạnh chung
AC < CF
Suy ra: \(\widehat {{O_1}} < \widehat {{O_3}}\) (hai tam giác có 2 cạnh bằng nhau từng đôi một, cạnh thứ 3 không bằng nhau, đối diện cạnh lớn hơn là góc lớn hơn).
Advertisements (Quảng cáo)
sđ \(\overparen{AE}\) = \(\widehat {{O_1}}\)
sđ \(\overparen{EF}\) \( = \widehat {{O_3}}\)
Suy ra: \(\overparen{AE}\) < \(\overparen{EF}\).
Câu 12: Cho đường tròn tâm O. Trên nửa đường tròn bán kính AB lấy hai điểm C, D. Từ C kẻ vuông góc với AB, nó cắt đường tròn tại điểm thứ hai là E. Từ A kẻ vuông góc với DC, nó cắt đường tròn tại điểm thứ hai là F.
Chứng minh rằng:
a) Hai cung nhỏ CF và DB bằng nhau.
b) Hai cung nhỏ BF và DE bằng nhau
c) DE = BF.

a) ∆ AFB nội tiếp trong (O) có
AB là đường kính nên ∆ AFB vuông tại F.
\( \Rightarrow BF \bot AK\)
\(AK \bot CD\) (gt)
Suy ra: BF // CD
\( \Rightarrow \) \(\overparen{BD}\) = \(\overparen{CF}\) (hai cung chắn giữa hai dây song song thì bằng nhau)
b) \(AB \bot CE\) tại điểm H nên C và H đối xứng qua trục AB.
\( \Rightarrow \) \(\overparen{BC}\) = \(\overparen{BE}\)
\(\overparen{CF}\) = \(\overparen{BD}\) (chứng minh trên)
Suy ra: \(\overparen{BC}\) + \(\overparen{CF}\) = \(\overparen{BE}\) + \(\overparen{BD}\)
Hay \(\overparen{BF}\) = \(\overparen{DE}\)
c) \(\overparen{BF}\) = \(\overparen{DE}\) (chứng minh trên)
d) BF = DE(hai cung bằng nhau căng hai dây bằng nhau).
Câu 13: Cho đường tròn (O). Gọi I là điểm chính giữa dây cung AB (Không phải là cung nửa đường tròn) và H là trung điểm của dây AB. Chứng minh rằng đường thẳng IH đi qua tâm O của đường tròn.
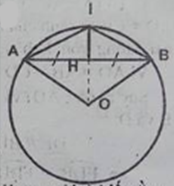
Ta có: \(\overparen{IA}\) = \(\overparen{IB}\)(gt)
\( \Rightarrow IA = IB\) (2 cung bằng nhau căng 2 dây bằng nhau)
\( \Rightarrow I\) nằm trên đường trung trực của AB
OA = OB (bán kính (O)
\( \Rightarrow O\) nằm trên đường trung trực của AB
Suy ra: OI là đường trung trực của AB
H là trung điểm của AB, do đó OI đi qua trung điểm H
Vậy 3 điểm I, H, O thẳng hàng.

