Câu 14: Cho đường tròn (O; R). Hãy vẽ hai cung (không phải là cung lớn) biết rằng cung này có số đo gấp ba lần số đo cung kia và có dây căng cung dài gấp đôi dây căng cung kia.
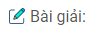
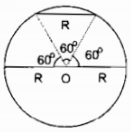
Vì cung không phải là cung lớn nên hai cung đó có thể là cung nhỏ hoặc cung nửa đường tròn. Ta có cung nửa đường tròn có số đo bằng 1800 và dây cung bằng 2R, cung tròn 600 nên có góc ở tâm bằng 600.
Tam giác tạo với 2 bán kính đi qua 2 đầu mút cong là một tam giác đều nên dây giương cung bằng bán kính R. Vậy nửa đường tròn và cung 600 thỏa mãn bài toán.
Câu 2.1: Cho đường tròn tâm O bán kính R. Vẽ góc ở tâm \(\widehat {AOB} = {80^0}\), vẽ góc ở tâm \(\widehat {BOC} = {120^0}\) kề với \(\widehat {AOB}\).
So sánh và sắp xếp độ dài AB, BC, CA theo thứ tự tăng dần.
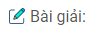
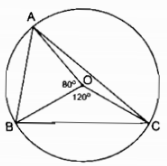
Ta có: \(\widehat {AOB} = {80^0}\); \(\widehat {BOC} = {120^0}\)
Suy ra: \(\widehat {AOC} = {160^0}\)
sđ \(\overparen{AB}\) \( = \widehat {AOB}\)
Advertisements (Quảng cáo)
sđ \(\overparen{BC}\) \( = \widehat {BOC}\)
sđ \(\overparen{AC}\) \( = \widehat {AOC}\)
\(\widehat {AOB} < \widehat {BOC} < \widehat {AOC}\)
Suy ra \(\overparen{AB}\) < \(\overparen{BC}\) < \(\overparen{AC}\)
Suy ra: AB < BC < AC
Câu 2.2: Cho hình thoi ABCD. Vẽ đường tròn tâm A, bán kính AD. Vẽ đường tròn tâm C, bán kính CB. Lấy điểm E bất kỳ trên đường tròn tâm A (không trùng với B và D), điểm F trên đường tròn tâm C sao cho BF song song với DE. So sánh hai cung nhỏ DE và BF.
Advertisements (Quảng cáo)
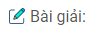
Ta có (A; AD) và (C; CB) có bán kính AD = CB là cạnh của hình thoi ABCD nên hai đường tròn đó bằng nhau.
Vì AD = AB = CD = CB
Suy ra (A; AD) và (C; CB) cắt nhau tại B và D.
DE // BF (gt)
\( \Rightarrow \widehat {EDB} = \widehat {FBD} \Rightarrow \widehat {EDA} + \widehat {ADB} = \widehat {FBC} + \widehat {CBD}\)
\(\widehat {ADB} = \widehat {CBD}\) (tính chất hình thoi)
Suy ra: \(\widehat {EDA} = \widehat {FBC}\) (1)
∆ADE cân tại A \( \Rightarrow \widehat {EAD} = {180^0} – 2\widehat {EDA}\) (2)
∆CBF cân tại C \( \Rightarrow \widehat {BCF} = {180^0} – 2\widehat {FBC}\) (3)
Từ (1), (2) và (3) suy ra: \(\widehat {EAD} = \widehat {BCF}\)
sđ \(\overparen{DE}\) \( = \widehat {EAD}\)
sđ \(\overparen{BF}\) \( = \widehat {BCF}\)
Vì (A; AD) và (C; CB) bằng nhau nên \(\overparen{DE}\) = \(\overparen{BF}\)

