Câu 7: Cho hai đường tròn (O) và (O’) cắt nhau tại A, B. Đường phân giác của góc OBO’ cắt các đường tròn (O), (O’) tương ứng tại C, D.
Hãy so sánh các góc ở tâm BOC và BO’D.
Sử dụng các tam giác cân OBC, O’BD.
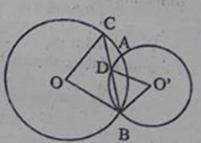
Trong (O) ta có:
\(\Delta OBC\) cân tại O (vì OB = OC bán kính)
\( \Rightarrow \widehat {BOC} = {180^0} – 2.\widehat {OBC}\) (1)
Trong (O’) ta có
\(\Delta BO’D\) cân tại O’ (vì O’D = O’D bán kính)
\( \Rightarrow \widehat {BO’D} = {180^0} – 2.\widehat {O’BD}\) (2)
\(\widehat {OBC} = \widehat {O’BD}\) (vì BC là phân giác của \(\widehat {OBO’}\)) (3)
Từ (1), (2) và (3) suy ra: \(\widehat {BOC} = \widehat {BO’D}\).
Câu 8: Trên một đường tròn, có cung AB bằng 1400, cung AD nhận B làm điểm chính giữa, cung CB nhận A là điểm chính giữa. Tính số đo cung nhỏ CD và cung lớn CD.
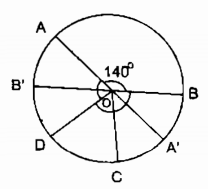
Ta có: cung AB = cung BD = cung AC (gt)
\( \Rightarrow \widehat {AOB} = \widehat {BOD} = \widehat {AOC} = {180^0}\)
Kẻ đường kính AA’, BB’ ta có:
\(\widehat {AOB} + \widehat {AOB’} = {180^0}\) (hai góc kề bù)
\( \Rightarrow \widehat {AOB’} = {180^0} – \widehat {AOB} = {180^0} – {140^0} = {40^0}\)
Suy ra: \(\widehat {BOA’} = \widehat {AOB’} = {40^0}\) (hai góc đối đỉnh)
\(\widehat {B’OD} + \widehat {BOD} = {180^0}\) (hai góc kề bù)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat {B’OD} = {180^0} – \widehat {BOD} = {180^0} – {140^0} = {40^0}\)
\(\widehat {AOC} = \widehat {AOB’} + \widehat {B’OD} + \widehat {DOC}\)
\( \Rightarrow \widehat {DOC} = \widehat {AOC} – \widehat {AOB’} – \widehat {B’OD} = {140^0} – {40^0} – {40^0} = {60^0}\)
sđ cung CD (nhỏ) = \(\widehat {COD} = {60^0}\)
sđ cung CD (lớn) = sđ cung CD (nhỏ) = 3600 – 600 = 3000
Câu 9: Cho C là một điểm nằm trên cung lớn AB của đường tròn (O). Điểm C của cung lớn AB thành hai cung AC và CB. Chứng minh rằng cung lớn AB có sđ cung AB = sđ cung AC = sđ cung CB.
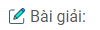Xét 3 trường hợp:
a) Tia OC nằm trong góc đối đỉnh của góc ở tâm AOB.
b) Tia OC trùng với tia đối của một cạnh của góc ở tâm AOB
c) Tia OC nằm trong một góc kề bù với góc ở tâm AOB
a) Trường hợp tia OC nằm trong góc đối đỉnh với \(\widehat {AOB}\)
Kẻ đường kính CD
Advertisements (Quảng cáo)
Suy ra: OD nằm giữa OA và OB nên điểm D nằm trên cung nhỏ cung AB
\( \Rightarrow \) sđ cung AD (nhỏ) + sđ cung BD (nhỏ) = sđ cung AB (nhỏ) (1)
Vì OA nằm giữa OC và OD nên điểm A nằm trên cung nửa đường tròn CD.
\( \Rightarrow \) sđ cung AD (nhỏ) + sđ cung AC (nhỏ) = 1800 (2)
Vì OB nằm giữa OC và OD nên điểm B nằm trên cung nửa đường tròn CD.
\( \Rightarrow \) sđ cung BD (nhỏ) + sđ cung BC (nhỏ) = 1800 (3)
Cộng từng vế (2) và (3):
sđ cung AD (nhỏ) + sđ cung AC (nhỏ) + sđ cung BD (nhỏ) + sđ cung BC (nhỏ) = 3600 (4)
Từ (1) và (4) suy ra: sđ cung AC (nhỏ) + sđ cung BC (nhỏ) + sđ cung AB (nhỏ) = 3600
\( \Rightarrow \) sđ cung AC (nhỏ) + sđ cung BC (nhỏ) = 3600 – sđ cung AB (nhỏ)
Mà 3600 – sđ cung AB (nhỏ) = sđ cung AD (lớn)
Vậy với cung lớn AB ta có: sđ cung AB = sđ cung AC + sđ cung BC
b)
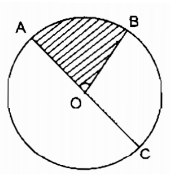
Trường hợp tia OC trùng với tia đối của một cạnh của góc ở tâm AOB ta có:
\(\widehat {AOB} + \widehat {BOC} = {180^0}\); $\widehat {AOC} = {180^0}\)
\( \Rightarrow \widehat {AOB} + \widehat {BOC} + \widehat {AOC} = {360^0}\)
\( \Rightarrow \widehat {AOC} + \widehat {BOC} = {360^0} – \widehat {AOB}\)
Suy ra: sđ cung AB + sđ cung BC (nhỏ) = 3600 – sđ cung AB (nhỏ)
Vậy với cung lớn AB ta có: sđ cung AB = sđ cung AC (nhỏ) + sđ cung BC
c)
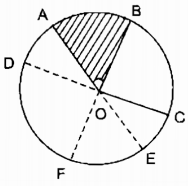
Trong hợp tia OC nằm trong góc kề bù với góc ở tâm AOB, kẻ đường kính AE.
Theo trường hợp b ta có:
sđ cung AB (lớn) = sđ cung AE (nhỏ) + sđ cung BE (nhỏ)
Ta xét trường hợp C nằm trên cung nhỏ EB:
sđ cung EB (nhỏ) = sđ cung EC (nhỏ) + sđ cung CB (nhỏ)
\( \Rightarrow \) sđ cung AB (lớn) = sđ cung AE + sđ cung EC (nhỏ) + sđ cung CB (nhỏ)
Theo kết quả trường hợp b ta có:
sđ cung AE + sđ cung EC (nhỏ)= sđ cung AC (lớn)
Vậy với cung AB lớn ta có: sđ cung AB = sđ cung AC + sđ cung CB
Trong trường hợp OC nằm trên góc đối với góc ở tâm \(\widehat {BOE}\) chứng minh tương tự.
Trong trường hợp OC nằm trên góc đối đỉnh với góc ở tâm \(\widehat {AOB}\) chứng minh ở trường hợp a.
