Bài 47: Khoảng 200 năm trước, hai nhà khoa học Pháp là Clô-zi-ut (Clausius) và Cla-pay-rông (Clapeyron) đã thấy rằng áp lực P của hơi nước (tính bằng milimét thủy ngân, viết tắt là mmHg) gây ra khi nó chiếm khoảng trống phía trên của mặt nước chứa trong một bình kín được tính theo công thức: P = a x \({10^{{k \over {t + 273}}}}\), trong đó t là nhiệt độ C của nước, a và k là những hằng số. Cho biết \(k \approx – 2258,624\).
a) Tính a biết rằng khi nhiệt độ của nước là 100oC thì áp lực của hơi nước là 760 mmHg (tính chính xác đến hàng phần chục).
b) Tính áp lực của hơi nước khi nhiệt độ của nước là \({40^0}C\) (tính chính xác đến hàng phần chục).
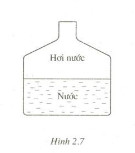
a) Khi nhiệt độ của nước là t = \({100^0}C\) thì P = 760. Do đó ta có phương trình (ẩn a) \(760 = a{.10^{{{ – 2258,624} \over {373}}}}\).
Từ đó ta có \(a \approx 86318884,4\).
b) \(P = 86318884,{4.10^{{{ – 2258,624} \over {313}}}} \approx 52,5\) mmHg.
Bài 48: Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to 0} {{{e^2} – {e^{3x + 2}}} \over x}\)
b) \(\mathop {\lim }\limits_{x \to 0} {{{e^{2x}} – {e^{5x}}} \over x}\)
a) \(\mathop {\lim }\limits_{x \to 0} {{{e^2} – {e^{3x + 2}}} \over x} = \mathop {\lim }\limits_{x \to 0} {{{e^2}\left( {1 – {3^{3x}}} \right)} \over x} \)
Advertisements (Quảng cáo)
\(= – 3{e^2}.\mathop {\lim }\limits_{x \to 0} {{{e^{3x}} – 1} \over {3x}} = – 3{e^2}\).
b) \(\mathop {\lim }\limits_{x \to 0} {{{e^{2x}} – {e^{5x}}} \over x} = \mathop {\lim }\limits_{x \to 0} \left( {{{{e^{2x}} – 1} \over x} – {{{e^{5x}} – 1} \over x}} \right) = 2 – 5 = – 3\).
Bài 49: Tính đạo hàm của các hàm số sau:
a) \(y = \left( {x – 1} \right){e^{2x}}\);
b) \(y = {x^2}.\sqrt {{e^{4x}} + 1} ;\)
Advertisements (Quảng cáo)
c) \(y = {1 \over 2}\left( {{e^x} – {e^{ – x}}} \right);\)
d) \(y = {1 \over 2}\left( {{e^x} + {e^{ – x}}} \right);\)
a) \({y’} = {e^{2x}} + \left( {x – 1} \right).2{e^{2x}} = \left( {2x – 1} \right).{e^{2x}}\)
b) \({y’} = 2x\sqrt {{e^{4x}} + 1} + {x^2}.{{4{e^{4x}}} \over {2.\sqrt {{e^{4x}} + 1} }} = {{2x\left[ {\left( {x + 1} \right){e^{4x}} + 1} \right]} \over {\sqrt {{e^{4x}} + 1} }}\)
c) \({y’} = {1 \over 2}\left( {{e^x} + {e^{ – x}}} \right)\)
d) \({y’} = {1 \over 2}\left( {{e^x} – {e^{ – x}}} \right)\)
Bài 50: Trong các hàm số sau đây, hàm số nào đồng biến, hàm số nào nghịch biến trên R?
a) \(y = {\left( {{\pi \over 3}} \right)^x}\);
b) \(y = {\left( {{3 \over {\sqrt 2 + \sqrt 3 }}} \right)^x}\);
a) Hàm số \(y = {\left( {{\pi \over 3}} \right)^x}\) đồng biến vì \({\pi \over 3} > 1\).
b) Hàm số \(y = {\left( {{3 \over {\sqrt 2 + \sqrt 3 }}} \right)^x}\) nghịch biến vì \({3 \over {\sqrt 2 + \sqrt 3 }} = 3\left( {\sqrt 3 – \sqrt 2 } \right) < 1\).

