Bài 43: a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số: \(y = – {x^4} + 2{x^2} – 2\)
b) Tùy theo các giá trị của m, hãy biện luận số nghiệm của phương trình \( – {x^4} + 2{x^2} – 2 = m\).
c) Viết phương trình tiếp tuyến tại các điểm uốn của đồ thị ở câu a)
Gỉải
a) TXĐ: \(D =\mathbb R\)
\(\eqalign{
& \mathop {\lim }\limits_{x \to \pm \infty } y = – \infty \cr
& y’ = – 4{x^3} + 4x = – 4x\left( {{x^2} – 1} \right);\cr&y’ = 0 \Leftrightarrow \left[ \matrix{
x = 0,\,\,\,\,\,\,y\left( 0 \right) = – 2 \hfill \cr
x = \pm 1,\,\,\,\,y\left( { \pm 1} \right) = – 1 \hfill \cr} \right. \cr} \)
Bảng biến thiên:
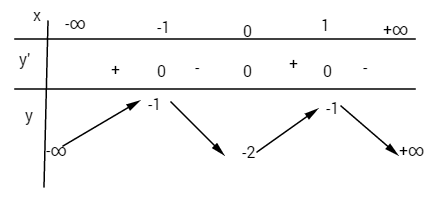
Hàm đồng biến trên các khoảng \(\left( { – \infty ; – 1} \right)\) và \(\left( {0;1} \right)\);
Hàm số nghịch biến trên các khoảng \((-1;0)\) và \(\left( {1; + \infty } \right)\)
Hàm số đạt cực đại tại các điểm \(x = -1 ; x = 1\);
Giá trị cực đại \(y\left( { \pm 1} \right) = – 1\). Hàm số đạt cực tiểu tại điểm \(x = 0\), giá trị cực tiểu \(y(0) = -2\).
\(\eqalign{
& y” = – 12{x^2} + 4 = – 4\left( {3{x^2} – 1} \right) \cr
& y” = 0 \Leftrightarrow x = \pm {1 \over {\sqrt 3 }};\,\,y\left( { \pm {1 \over {\sqrt 3 }}} \right) = {{ – 13} \over 9} \cr} \)
Xét dấu y”
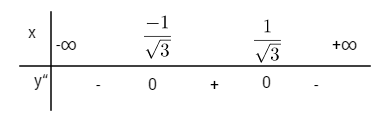
Đồ thị có hai điểm uốn \({I_1}\left( { – {1 \over {\sqrt 3 }}; – {{13} \over 9}} \right)\) và \({I_2}\left( {{1 \over {\sqrt 3 }}; – {{13} \over 9}} \right)\)
Điểm đặc biệt \(x = 2 \Rightarrow y = – 10\)
Đồ thị nhận trục tung làm trục đối xứng.
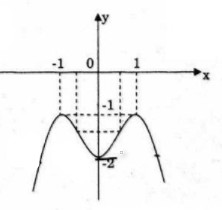
b) Số nghiệm của phương trình chính là số giao điểm của đồ thị (C) hàm số \(y = – {x^4} + 2{x^2} – 2\) với đường thẳng \(y = m\).
Dựa vào đồ thị ta có kết quả sau:
– Nếu \(m < -2\) thì phương trình có \(2\) nghiệm;
– Nếu \(m = -2\) thì phương trình có \(3\) nghiệm;
– Nếu \(-2 < m < -1\) thì phương trình có \(4\) nghiệm;
– Nếu \(m = -1\) thì phương trình có \(2\) nghiệm;
– Nếu \(m> -1\) thì phương trình vô nghiệm.
c) Đồ thị có hai điểm uốn \({I_1}\left( { – {1 \over {\sqrt 3 }}; – {{13} \over 9}} \right)\) và \({I_2}\left( {{1 \over {\sqrt 3 }}; – {{13} \over 9}} \right)\)
phương trình tiếp tuyến của đồ thị \({I_1}\) là:
\(\eqalign{
& y + {{13} \over 9} = y’\left( { – {1 \over {\sqrt 3 }}} \right)\left( {x + {1 \over {\sqrt 3 }}} \right) \cr&\Leftrightarrow y + {{13} \over 9} = {{ – 8} \over {3\sqrt 3 }}\left( {x + {1 \over {\sqrt 3 }}} \right) \cr
& \Leftrightarrow y = {{ – 8} \over {3\sqrt 3 }}x – {7 \over 3} \cr} \)
Tương tự tiếp tuyến của đồ thị \({I_2}\) là : \(y = {8 \over {3\sqrt 3 }}x – {7 \over 3}\)
Bài 44: Khảo sát sự biến thiên và vẽ đồ thị hàm số sau:
a) \(y = {x^4} – 3{x^2} + 2\) b) \(y = – {x^4} – 2{x^2} + 1\)
Gỉải
a) TXĐ: \(D =\mathbb R\)
\(\eqalign{
& \mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \cr
& y’ = 4{x^3} – 6x;\cr&y’ = 0 \Leftrightarrow \left[ \matrix{
x = 0;\,\,\,\,\,y\left( 0 \right) = 2 \hfill \cr
x = \pm \sqrt {{3 \over 2}} ;\,\,y\left( { \pm \sqrt {{3 \over 2}} } \right) = – {1 \over 4} \hfill \cr} \right. \cr} \)
Advertisements (Quảng cáo)
Bảng biến thiên:
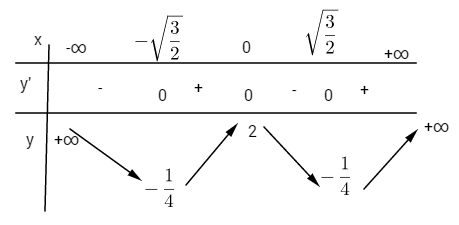
\(y” = 12{x^3} – 6;\)
\(y” = 0 \Leftrightarrow x = \pm \sqrt {{1 \over 2}} ;\,y = \left( { \pm \sqrt {{1 \over 2}} } \right) = {3 \over 4}\)
Xét dấu \(y”\)
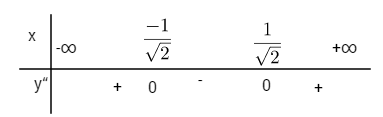
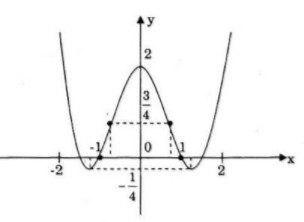
Đồ thị có hai điểm uốn \({I_1}\left( { – \sqrt {{1 \over 2}} ;{3 \over 4}} \right)\) và \({I_2}\left( {\sqrt {{1 \over 2}} ;{3 \over 4}} \right)\)
Điểm đặc biệt: \(x = \pm 1 \Leftrightarrow y = 0,x = \pm \sqrt 2 \Leftrightarrow y = 0.\)
Đồ thị: Đồ thị nhận trục tung làm trục đối xứng.
b) TXĐ: \(D =\mathbb R\)
\(\eqalign{
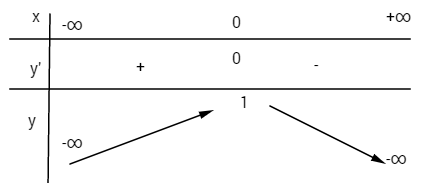
& \mathop {\lim }\limits_{x \to \pm \infty } y = – \infty \cr
& y’ = – 4{x^3} – 4x = – 4x\left( {{x^2} + 1} \right) \cr
& y’ = 0 \Leftrightarrow x = 0;y\left( 0 \right) = 1 \cr} \)
Bảng biến thiên:
\(y” = – 12{x^2} – 4 = – 4\left( {3{x^2} + 1} \right) < 0\) với mọi \(x\)
Đồ thị không có điểm uốn.
Điểm đặc biệt \(x = \pm 1 \Rightarrow y = – 2\)
Đồ thị:
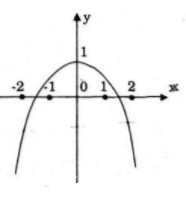
Đồ thị nhận trục tung làm trục đối xứng.
Bài 45: a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số: \(y = {x^3} – 3{x^2} + 1\).
b) Tùy theo các giá trị của \(m\), hãy biện luận số nghiệm của phương trình: \({x^3} – 3{x^2} + m + 2 = 0\)
Advertisements (Quảng cáo)
a) TXĐ: \(D =\mathbb R\)
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\,\mathop {\lim }\limits_{x \to – \infty } y = – \infty \cr
& y’ = 3{x^2} – 6x = 3x\left( {x – 2} \right);\cr&y’ = 0 \Leftrightarrow \left[ \matrix{
x = 0;\,\,\,\,y\left( 0 \right) = 1 \hfill \cr
x = 2;\,\,\,\,y\left( 2 \right) = – 3 \hfill \cr} \right. \cr} \)
Bảng biến thiên:
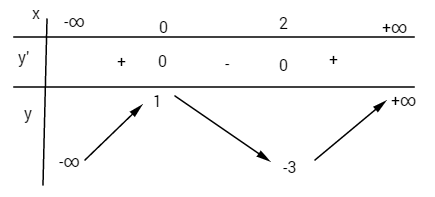
Hàm số đồng biến trên các khoảng \(\left( { – \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\); nghịch biến trên khoảng \((0;2)\).
Hàm số đạt cực đại tại điểm \(x = 0\), giá trị cực đại \(y(0) = 1\); hàm số đat cực tiểu tại điểm \(x = 2\), giá trị cực tiểu \(y(2) = -3\).
\(y” = 6x – 6;\,y” = 0 \Leftrightarrow x = 1;\,y\left( 1 \right) = – 1\)
Xét dấu \(y”\)
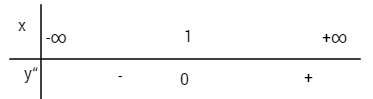
Điểm uốn của đồ thị \(I(1;-1)\)
Điểm đặc biệt \(x = – 1 \Rightarrow y = – 3\)
Đồ thị: đồ thị nhận điểm \(I(1;-1)\) làm tâm đối xứng.
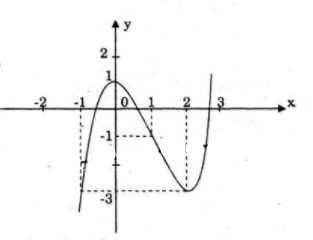
b) Ta có: \({x^3} – 3{x^2} + m + 2 = 0 \Leftrightarrow {x^3} – 3{x^2} + 1 = – m – 1\)
Số nghiệm của phương trình trên bằng số giao điểm của đồ thị hàm số \(y = {x^3} – 3{x^2} + 1\) và
đường thẳng \(y = – m -1\). Dựa vào đồ thị ta có:
– Nếu \( – m – 1<-3\Rightarrow m>2\) thì phương trình có \(1\) nghiệm.
– Nếu \(-m-1=-3\Rightarrow m=2\) thì phương trình có \(2\) nghiệm.
– Nếu \(-3< -m-1<1\Rightarrow -2<m<2\) thì phương trình có \(3\) nghiệm.
– Nếu \(-m-1=1\Rightarrow m=-2\) thì phương trình có \(2\) nghiệm
– Nếu \(-m-1>1\Rightarrow m<-2\) thì phương trình có \(1\) nghiệm.

